Note

记录初探CF竞赛的经历.

在朋友的邀请下开始打Codeforces比赛了, 到目前为止参加了Round 973和974两场. 由于不熟悉赛程什么的, 加上12点左右就要睡觉, 只能打1个半小时左右, 所以成绩不算很好看. 还在修炼当中.

Round 973 - Div 2

最终的成绩如下:

A 打卡题-搅拌机榨水果

了解题意后只需要求一个min就可以了.

用cpp写的时候很不熟悉, 研究缓冲区之类的东西花了些时间, vscode的run code功能还坏掉了. 读题和提交也慢, 所以20多分钟才写完.

B 拳击手互殴

n名拳击手进行n-1场比赛, 右边的拳击手会将左边的拳击手淘汰, 同时自己的数值也降低. 最终剩下的必定是最右边的拳击手. 要求最终的选手的数值最大.

一开始往贪心和动态规划之类的地方想, 满脑子都是递归之类的东西. 研究了许久之后, 发现了"最后一位"和"倒数第二位"两个位置的奇妙. 于是从数学上想清楚了思路.

编写代码也很简单, 但是交上去老是过不了. 事后才发现是longlong的问题.

十年OI一场空, 不开longlong见祖宗

C hacking密码

需要通过最多2n次"是否包含子列"的询问, 将n位的密码构建出来.
很有意思的题目. 样例给出来的"询问方式"都是直接问出答案的. 可能是因为正常询问就相当于进行了提示吧.

一开始往树和信息熵的方面想, 同时尝试分析了几个例子, 却总是不得要领.

后来打完974的晚上横竖睡不着, 躺在床上把它想了出来.

核心思想就是, 用至多两次询问, 将"确定的密码位数"增加一位. 例如, 从"0"开始询问. 已知密码内包含串x的情况下, 分别询问x0, x1. 如果其中一个为"包含", 那么已知的字串长度增加了1; 如果两个都不包含, 说明x一定位于密码末尾, 接下来挨个询问其左边的密码即可. 如此以来, 总能在2n次询问中解决问题.

见到题目的第一时间把它想的太复杂了, 思路总是往"形式化分析该问题"上面靠, 导致老是在想"输出的策略本身是一个树, 各种策略在一起又构成一个树"之类的事情. 实际上应该先依靠直觉进行探索.

D 抹平贫富差距

类似"流水从左往右冲刷沙堆"的情况, 高度可以"单向进行移动".

一开始也是想着动态规划和递归什么的. 后面躺在床上发现了其中玄妙.

秘诀就是, 从最左边出发, 将"几乎等高"的柱子看成一组, 同时, 组与组之间在某种情况下可以合并.
这样一来, 一开始就有n组柱子, 每组含有一个成员.

  • 当遇到"ai<ai+1a_i < a_{i+1}"的情况时, 左右无法进行合并.
  • 当遇到"ai>ai+1a_i > a_{i+1}"的情况时, 将新出现的ai+1a_{i+1}并入aia_{i}中.

类似递归排序的方法, 总是对"新加入的组"进行判断, 如此反复进行下去. 最终能够用线性的时间解决问题.
代码编写好像不是那么显然, 但也不算太复杂.

Others

  • 其他的题目还没有看, 也不打算看了.
  • 有时间找找jiangly的视频, 学习一下这些题的解法.

Round 974 - Div 3

最终的成绩如下:

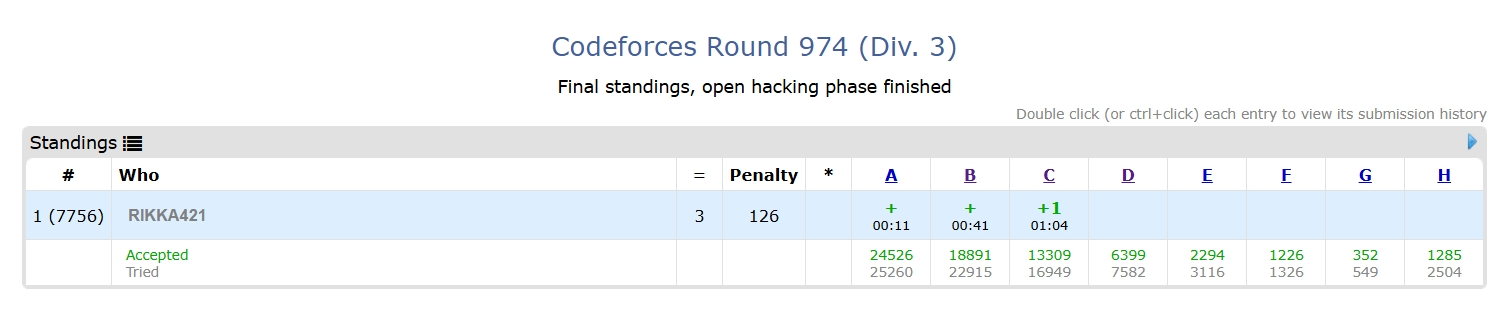
  • 做了1h40min吧, 一直干到了00:30左右.
  • 最后还剩下20min, 感觉写下去是可以把第4题写出来的, 因为就差最后一点代码了. 但是也许不行.
  • 总之最后成绩是3题.

A 富人全拿走, 穷人送一颗 - 打卡题

  • 罗宾汉会抢走富人的所有钱, 并送给财产为0的穷人一枚金币.
  • 给出当前财产情况, 问罗宾汉劫富济贫之后, 财产情况是怎么样的.

对每个人, 简单进行判断即可. 复杂度是线性的

B 足够不平等, 召唤罗宾汉

  • 给出当前财产情况, 最富有的人会额外得到一笔x的财富
  • 穷人: “财产严格小于平均水平的一半”
  • 民心可用: “穷人数量严格大于人数的一半”
  • 当民心可用时, 罗宾汉就会出现

问, x最少需要为多少, 才能够召唤罗宾汉? 输出x.

  • 当罗宾汉无论如何也无法被召唤, 输出-1
  • 当罗宾汉不需要给予x就已经可以出现, 输出0
  • 其余情况, 输出那个最小的x

排序之后求出中位数, 之后做O(1)O(1)的计算即可. 以上是最直接的想法.

想出来没有花时间, 但是写代码的时候处理细节花了很久.

理论上, 我们可以用O(n)O(n)的算法来求出中位数, 然后进行求解. 从而得到最优的线性解法.

采用大顶小顶两个堆进行求解. 利用"堆的插入操作是对数复杂度"这一性质, 可以形式化证明其复杂度是线性的.

C 叶子生又落, 求出奇偶性

  • 树木在第ii天会长出iii^i个叶子
  • 长出的叶子会在kk天之后凋落
  • 给出n,kn, k, 求出第nn天时, 树木上叶子数的奇偶性.

先直接得到奇偶数列"每天长出的叶子", 然后得到其前n项和的奇偶数列SnS_n. SnS_{n}的奇偶性是周期的, 可在常数时间内给出. 之后, 对Sn−Sn−kS_n - S_{n - k}的奇偶性进行考虑即可.
最终的复杂度是常数的.

讨论奇偶性花了和调代码花了不少时间. 教训是在数学上的性质和原理一开始没有想明白, 就急匆匆地去写代码了. 后面才想清楚"前n项和"来简洁表述的想法.

D 哥哥与姑姑探访, 求出最值

  • 罗宾汉在nn天内进行kk次侠盗活动. 每次活动会持续一段时间
  • 侠盗活动持续时间通过一个区间给出
  • 哥哥和姑姑分别拜访一段时间, 拜访持续dd天
  • 要求: 哥哥拜访期间, 遇到的侠盗活动尽可能多; 姑姑拜访期间, 遇到的侠盗活动尽可能少.
  • 给出两人拜访的最佳时间. 若有多种选择, 选择拜访时间最早的选项.

一开始的思路是: 先将kk个区间排序, 之后用n的时间扫一遍, 将"每天正在持续的侠盗活动"的数组处理出来. 再之后, 根据单天的时间表, 通过滑窗的方式, 做取最值的处理, 将"区间内持续的侠盗活动"解出来.
思路和代码都有些繁琐, 写着很不舒服.

后面看了jiangly的解法, 是先将区间存下来, 再求出前n项和. 其中

  • 对区间左端点l做"减减"操作
  • 求出左端点的"后n项和", 即"从某天起, 还没开始的侠盗活动数目"
  • 求出右端点的"前n项和", 即"在某天前, 已经结束的侠盗活动数目"
  • 将两个前n项和相加, 得到"与当前区间无关的活动的数目"x
  • x越大, 说明区间内发生的活动数越少. 根据x确定最佳日期即可.

这个想法其实略微有点不自然. 最自然的做法应该是"左端点求前n项和, 右端点求后n项和.“, 然后求出"区间内正在进行的侠盗活动数”, 再进行判断.
不过这些都是细节了. 主要需要学习的是, 通过前n项和的处理, 使得"关于区间数值的求解"变成常数时间操作. 因此, 在遇到与区间有关的题目时, 应该考虑求和操作.

此外, yp讲述的差分思路也很有意思, 通过类似桶排序的做法, 用O(n)的时间"将k个区间压成了一个区间", 比我的方法简单且快捷了许多. 虽然这种方法在压完之后, 还是得处理"滑窗"之类的事情, 所以不够简洁优雅.

总结

革命尚未成功, 同志们还需努力. 憧憬成为CF高手 😉

backtop