LearnLog

Ch3 Lexical Analysis

编译原理的第三章笔记, 讲述了词法分析器的内容.

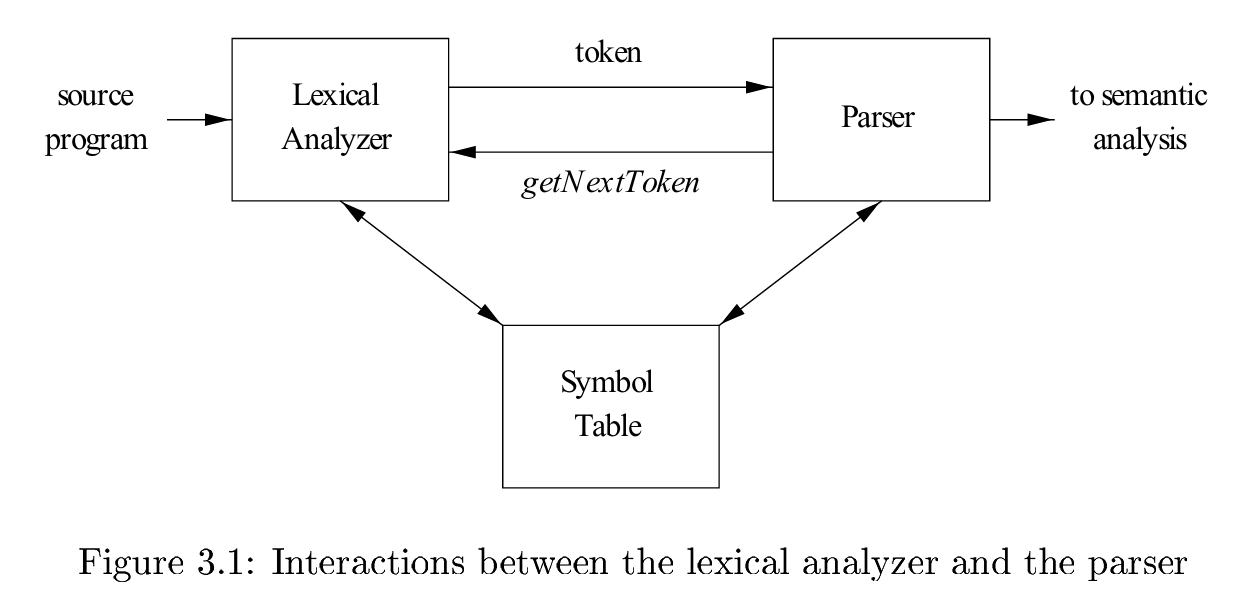
The Role of the Lexical Analyzer

词法分析器将字节流转换为tokens, 同时将一些变量信息保存在Symbol Table中.

Scanning
Lexical analysis

Lexical Analysis Versus Parsing

为何要将词法分析与解析(语法分析)显式地区分为两个环节?

Simplicity: 细分使得两个环节的设计都变得更简单.
Compiler effciency: 在lexical的环节, 可以用一些特别的技术, 来提高效率, 如buffer相关的技术.
Compiler portability: 提高可移植性. Lexical analyzer可以是设备相关的.

Tokens, Patterns, and Lexemes

A token is a pair consisting of a token name and an optional attribute value.
A pattern is a description of the form that the lexemes of a token may take.
A lexeme is a sequence of characters in the source program that matches the pattern for a token and is identified by the lexical analyzer as an instance of that token

Token类似类名, 它所包含的特性为pattern, 它的实例为许许多多的lexemes.

大部分语言中, token分为如下几类

关键字token: if, else, then等
操作符token: comparison等, 实例为>, < =等
identifiers token: id, 实例为各种变量名, 函数名
constant number token: number, 实例为0, 0.1, 3.14等
文本信息: literal等, 实例为// some word, "some string"等
punctuation symbol tokens: 各种标点符号token.

Attributes for Tokens

对于每一个token, 它们的lexeme都可以有很多个. 为了区分它们, 我们将其与一些info组合在一起, 这些info可能是包含许多信息的结构.
对于某些只可能含单个lexeme的token, 它们的info就不需要保存.

各个token的info各不相同, 例如id的info就是一个指向Symbol Table的指针, 而number则指向常量所在的地址.

Lexical Errors

一般无法在lexical的环节出现error. 如果出现了, 常见的处理方法是对剩余的input作delete / insert / replace / transpose操作, 直到遇到新的token.

Input Buffering

在扫描输入的时候, 我们总是需要读到下一个token的一部分内容, 才能确定当前的token已经结束. 因此, 我们采用two-buffer scheme 以及
"sentinels"的impove, 来更好地处理这种情况.

Buffer Pairs

两个buffer: 为了应对某个lexeme刚好处在buffer分界线的情况. (我们不考虑某个lexeme占据了整个buffer的情况)
两个指针: forward指针, 指向当前的index; lexemeBegin指针, 指向当前正在判断的lexeme的起始位置.

Sentinels

为了一致性, 我们将判断当前buffer是否结束的工作和判断当前读入的char的工作合并起来, 即添加特殊字符eof作为buffer结束的标志.

Specification of Tokens

Strings and Languages

与Automata中的内容相同, 此次只是简单罗列出定义.

An alphabet is any finite set of symbols
A string over an alphabet is a finite sequence of symbols drawn from that alphabet.
A language is any countable set of strings over some fixed alphabet.

substring and subsequence

substring: 字符串s删除任意前缀 / 后缀所得到的串

subsequence: 字符串删除0个或多个不一定连续的位所得到的串

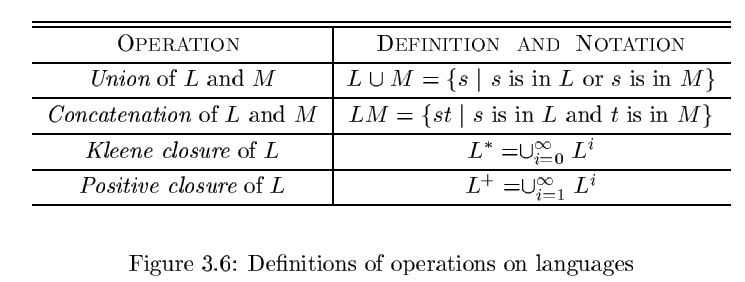
Operations on Languages

Languages上的一些操作. 由于languages是字符串的集合, 所以这些都是特殊的集合操作.

Regular Expressions

有了如上的集合操作作基础, 我们很容易就能得到正则表达式的形式化描述:
以某些字母表作为基础, 反复进行union, concatenation和Kleene closure操作而得到的新语言.

递归定义如下:
BASIS:

$\epsilon$ 是正则表达式, 同时 $L(\epsilon) = \{\epsilon\}$ 是只含空串的空语言
如果 $a$ 是字母表 $\Sigma$ 中的符号, 那么 $a$ 是正则表达式, 且 $L(a) = \{a\}$ .

INDUCTION:
如果 $r, s$ 是正则表达式, 且对应的语言为 $L(r), L(s)$ , 那么

$(r) | (s)$ 是对应于语言 $L(r) \cup L(s)$ 的正则表达式
$(r)(s)$ 是对应于语言 $L(r)L(s)$ 的正则表达式
$(r)^*$ 是对应于语言 $(L(r))^*$ 的正则表达式
$(r)$ 是对应于语言 $L(r) \cup L(s)$ 的正则表达式, 表明单纯添加括号不改变正则表达式所表示的语言

通过确定符号的优先级(如闭包操作优先级最高, 连接操作次之, 并操作优先级最低), 我们可以获得不含括号的正则表达式.

regular set: 能够被regular expression表示的语言.
若两个regular expression的regular set相等, 则称regular expression相等.
由此可以获得一些基本的代数性质:

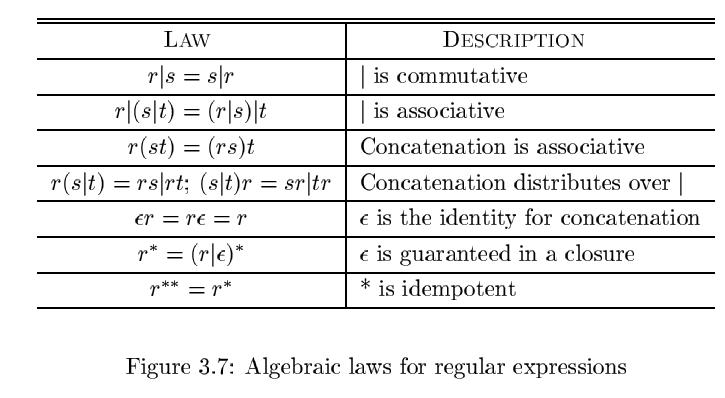
Regular Definitions

通过右箭头的方式, 来给某个正则表达式命名, 并通过已经命名的正则表达式不断向上构建, 最终得到包含复杂结构的式子.

Extensions of Regular Expressions

One or more instances. $r^* = r^+ | \epsilon$
Zero or one instance. $r? = r|\epsilon$
Character classes. $[a_1a_2...a_n] = a_1|a_2|...|a_n = [a_1$ - $a_n]$

Recognition of Tokens

定义了一个例子语言, 包括其pattern和tokens.

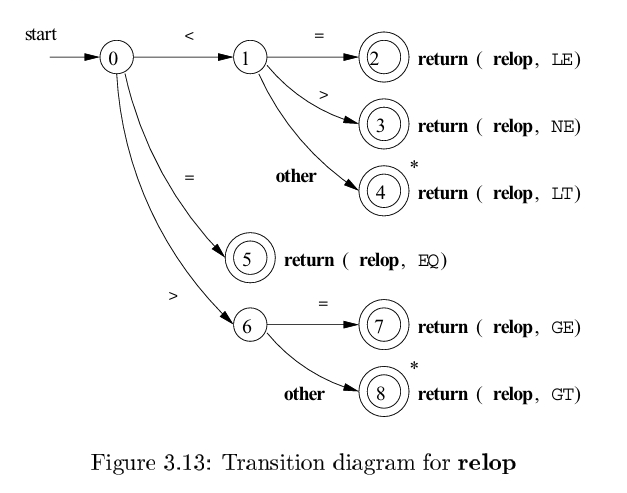
Transition Diagrams

一个DFA. 描述了例子语言的辨别token过程.

Recognition of Reserved Words and Identifiers

有两种方案:

预先将保留字保存到变量表中. 于是, 那些新加入的token就不可能是保留字, 只可能是id
单独为保留字建立transition diagrams

Completion of the Running Example

建立了unsigned numbers和whitespace的transition diagram

Architecture of a Transition-Diagram-Based Lexical Analyzer

对于单个transition diagram, 我们可以通过仔细的编排, 将其包装为一个函数.
为了用上每个transition diagram, 有如下的几种方案:

线性地, 一个接一个地尝试每个token, 在fail了之后将指针指向string头部, 并尝试下一个
并行化的, 将每个读入的字符同时输入给所有函数. 此时我们需要处理那些类似"thennextvalue"的问题, 即某些较短的token可能提前结束.
将所有transition diagrams合并为一个. 即将它们合并为一个巨大的DFA.

The Lexical-Analyzer Generator Lex

Use of Lex

Structure of Lex Programs

Conflict Resolution in Lex

The Lookahead Operator

Finite Automata

有穷自动机类似transition diagrams, 但是有一些不同

Finite Automata对于每个输入string, 只返回"yes" or “no”
Finite Automata有两类, NFA和DFA.

如下是关于NFA和DFA的一些形式化定义, 在Automata中已经给出, 此处不再赘述. 详见

[Compilers] Ch1 导论: Introduction | RIKKA’s Blog (rikka421.github.io)

Nondeterministic Finite Automata

Transition Tables

Acceptance of Input Strings by Automata

Deterministic Finite Automata

From Regular Expressions to Automata

Conversion of an NFA to a DFA

Simulation of an NFA

Effciency of NFA Simulation

Construction of an NFA from a Regular Expression

给出一个将正则表达式转换为NFA的算法.

The McNaughton-Yamada-Thompson algorithm to convert a regular expression to an NFA.

这个算法根据正则表达式的归纳定义, 同样的归纳进行构造, 很容易理解.

BASIS: 对于正则不等式 $\epsilon$ 和 $a$ , 分别构造仅含两个状态的NFA.