CH2 Finite Automata

关于有穷自动机, 包括DFA与NFA的形式化定义, DFA与Language一一对应的证明, 以及DFA与NFA的等价性的证明.

在这一章中, 我们将讨论两类自动机: 确定性有穷自动机(Deterministic Finite Automata)和非确定性有穷自动机(Nondeterministic Finite Automata), 以及与它们密切相关的一类语言: 正则语言(Regular Language).

此时, 正则语言以一种完全相关于自动机的方式被引入. 在下一章, 我们还会引入一类代数符号用于表示正则语言: RE(正则表达式). 同时, 我们会惊讶地发现, 自动机与正则语言的表达能力是完全等价的.

此外,

我们介绍了DFA, NFA, $\epsilon$ -NFA的定义,
以及它们延拓的转移函数的定义.
同时, 为了方便处理, 我们定义了 $\epsilon$ 闭包的概念.

然后, 我们大量应用了自然归纳法, 用于相关的定义和证明. 这一章之后, 我们可以发现,

DFA与NFA是可以互相转换的,
$\epsilon$ -NFA也可以转换为DFA.
同时, 由于这些证明是构造性地, 我们也能够直接地得到具体的转换方式.

2.1节介绍了一个银行的例子, 用于作为一个引入, 对于DFA的思想有一个较为直观的表现. 在此略过

总之, 让我们从确定性自动机DFA开始.

Deterministic Finite Automata

Definition of a Deterministic Finite Automaton

形式化定义: 我们用一个五元组来定义DFA

A = <Q, \Sigma, \delta, q_0, F>

$Q$ : 状态集合, 包括有穷个状态
$\Sigma$ : 动作集合, 包括有穷个动作信号
$\delta: Q\times \Sigma \rightarrow Q$ : 转移函数, 将状态与动作的二元组映射到下一个状态
$q_0$ : 起始状态
$F$ : 终止状态集合

Simpler Notations for DFA’s

A transition diagram: 转移图, 用点和边来表示状态与状态的转移.
A transition table: 用一个状态转移表来表示状态与状态的转移.

Extending the Transition Function to Strings

扩展定义, 从单步的转移函数扩展为对字符串的转移函数. 将延拓出的函数表示为

\hat{\delta} : Q \times S \rightarrow Q

定义是递归的:

$\hat{\delta}(q, \epsilon) = \delta(q, \epsilon) = q$ ,
对于非空的字符串 $s := xa$ , 定义 $\hat{\delta}(q, s) = \delta(\hat{\delta}(q, x), s)$

上面的定义很自然, 此处不作赘述.
定义延拓的转移函数是为了方便后续的证明. 转移函数是由已经定义好的五元组自然导出的结果.
实际推导中, 我们可以用转移矩阵反复相乘, 以求得各个长度字符串所对应的延拓转移函数

The Language of a DFA

直观上, 所有在DFA上运行后, 能够处于接收态的字符串, 都属于DFA所导出的 $L$ 集合. 形式化地:

L(A)= \{w | \hat{\delta}(q, w) \in F\}

此处, 我们对于一个已定义的DFA导出了一个语言集合 $L(A)$ .
后面我们还会发现, 对于一个定义好的语言集合 $L(A)$ , 同样能相应地导出一个DFA.

Nondeterministic Finite Automata

对于同一个输入, 能够同时转移到多个状态; 对于接收条件的判断, 只要终止时所处在的状态集合中, 包含有至少一个接收状态即可.
可以将其理解为"能够随意猜测方向, 且总是能猜对"的DFA.

形式化地, 我们同样定义一个五元组

A = <Q, \Sigma, \delta, q_0, F>

$Q$ : 状态集合, 包括有穷个状态
$\Sigma$ : 动作集合, 包括有穷个动作信号
$\delta: Q\times \Sigma \rightarrow 2^Q$ : 转移函数, 将状态与动作的二元组映射到下一个状态. 此处, 对于单个状态和单个输入信号, 返回的是一个状态集合而非单个状态.
$q_0$ : 起始状态
$F$ : 终止状态集合

The Extended Transition Function

对于延拓的转移函数, 由于原始转移函数在输出层面引入了状态的集合, 所以在对于延拓之后的转移函数, 其输入输出中的状态都是一个集合, 而非单个状态元素.

形式化地, 同样给出其归纳定义:

$\hat{\delta}(q, \epsilon) = \delta(q, \epsilon) = \{q\}$ ,
对于非空的字符串 $s := xa$ , 假定 $\hat{\delta}(q, x) =\{q_1,q_2, ..., q_k\}$ , 定义 $\hat{\delta}(q, s) = \cup_{i}^{k} \delta(q_i, s)$

The Language of an NFA

由于此时对于某个字符串 $w$ 和状态机 $NFA$ , 导出的结果是一个状态集合. 所以, 我们不能通过 $q_w\in F$ 来判断是否终止.

此时的判断条件变更为 $Q_w \cap F = \emptyset$ 是否成立.

形式化地

L(A) = \{w | \hat{\delta}(q_0, w) \cap F \neq \emptyset\}

Equivalence of Deterministic and Nondeterministic Finite Automata

等价性证明. 大致的思想是: 显式地考虑NFA在状态转移时产生的状态集合, 并将它们建模为一个DFA中的状态, 从而得到NFA到DFA的转换.

形式化地:
对于给定的NFA $N = (Q_N, \Sigma, \delta_N, q_0, F_N)$ , 我们考虑一个DFA $D = (Q_D, \Sigma, \delta_D, \{q_0\}, F_D)$ . 然后, 我们归纳地定义DFA的状态集合, 转移函数, 以及接收状态集合.
其中:

$\delta_D(S, a) = \cup_{p \in S} \delta_N(p, a)$
$Q_D$ 是 $Q_N$ 的一个子集, 由初始状态 $\{q_0\}$ 不断进行转移, 最终闭包产生. 状态个数的上界是 $2^n$ , 但是在大多数场景下, 被访问到的集合数目往往不会达到指数级别.
$F_D = \{Q \in Q_D| Q\cap Q_N \neq \emptyset\}$

$Q_D$ 更加形式化的定义为:

Q_D^{(0)} = \{q_0\}, Q_D^{(i+1)} = \cup_{a \in \Sigma}\delta_D(Q_D^{(i)}, a)

Q_D = \cup_{i}^{\infty} Q_D^{(i)}

在完成上面的定义后, 我们形式化地证明其等价性. 这个定理的证明是构造性的, 所以只是对定义的不断应用.

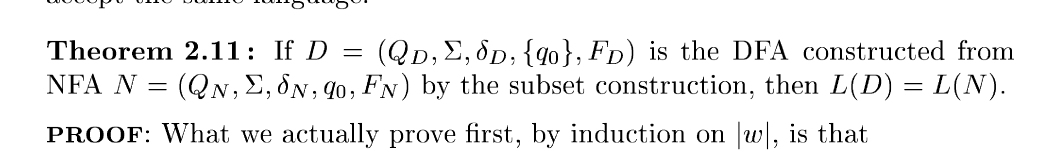
要证定理成立, 即证 $L(D) = L(N)$ .
要证集合相等, 需要从两方面证明. 我们要证明对于任意的字符串 $w\in \Sigma *$ , $w \in L(D)$ 等价于 $w \in L(N)$
即 $\hat{\delta_N} (q_0, w) \cup F_N \neq \emptyset$ 等价于 $\hat{\delta_D} (q_0, w) \in F_D$

为此, 我们先证明: 对于两个状态机, 延拓后的转移函数接收到相同的字符串时, 会给出相同的集合作为结果.

我们归纳地开始证明. 对于字符串的长度作归纳:

对于空字符串的情况, 根据定义显然有 $\delta_N (q_0, \epsilon) = \{q_0\}$ , $\delta_D (\{q_0\}, \epsilon) = \{q_0\}$ . 合乎条件.
对于任意字符串 $w:= xa$ , 假定 $\hat{\delta_N}(q_0, x) = \hat{\delta_D}(\{q_0\}, x) =\{q_1,q_2, ..., q_k\} = Q$ , 根据定义可以得到 $\hat{\delta_N}(q_0, w) = \hat{\delta_D}(\{q_0\}, w) = \hat{\delta_D}(Q, a) = \cup_{i}^{k} \delta_N(q_i, s)$ .

因此, 对于任意的输入字符串 $w$ , 我们有

\hat{\delta_N}(q_0, w) = \hat{\delta_D}(\{q_0\}, w)

于是根据定义, $\hat{\delta_N} (q_0, w) \cup F_N \neq \emptyset$ 等价于 $Q\cap Q_N \neq \emptyset$ 等价于 $Q\in F_D$ 等价于 $\hat{\delta_D} (q_0, w) \in F_D$ .

于是对任意 $w\in \Sigma *$ , $w \in L(D)$ 等价于 $w \in L(N)$ Q.E.D.

此时需要证明双向箭头. 箭头的一个方向在上面的定理中已经完成了证明; 另一个方向的箭头是显然的: 只需要将DFA的转移函数的输出转变为集合的形式即可(这些集合都是单元素集).
Q.E.D.

A Bad Case for the Subset Construction

可以发现, 这个NFA接收这样的语言, 语言中所有字符串的倒数第n个字符为1, 其余字符不做要求.

显然, 这个NFA转换得到的DFA至少需要包含 $2^n$ 个状态, 用于存储倒数n个字符的情况. 我们可以通过反证法, 利用鸽笼原理完成这个证明:

假设我们有一个DFA, 它接收上述的语言, 并且状态数目小于 $2^n$ .
此时, 我们发现, 对于字符串 $a = a_{n}a_{n-1}...a_{2}a_1$ , $b = b_{n}b_{n-1}...b_{2}b_1$ , $\hat{\delta}(q_0, a) = \hat{\delta}(q_0, b)$ 当且仅当 $a=b$ . 下面我们对这个论断进行证明:
对于论断"当 $a = b$ 时, $\hat{\delta}(q_0, a) = \hat{\delta}(q_0, b)$ ", 这是显然的.
对于论断"当 $a != b$ 时, $\hat{\delta}(q_0, a) != \hat{\delta}(q_0, b)$ , 我们采用反证法证明: 假设 $a != b$ , 此时必定有一个i使得 $a_i != b_i$ . 此时, 我们假设 $\hat{\delta}(q_0, a) = \hat{\delta}(q_0, b)$ , 同时构造出新的两个字符串 $a' = a_{n}a_{n-1}...a_{i}c_{i-1}...c_{2}c_{1}$ , $b' = b_{n}b_{n-1}...b_{i}c_{i-1}...c_{2}c_{1}$ . 由于两个字符串添加的是同一个尾缀, 同时 $\hat{\delta}(q_0, a) = \hat{\delta}(q_0, b)$ , 那么必定有 $\hat{\delta}(q_0, a') = \hat{\delta}(q_0, b')$ . 但是这是不可能的, 因为 $a', b'$ 的接收状态一定是相反的.
于是, 由于n位字符串 $a$ 可能有 $2^n$ 种, 同时当 $a != b$ 时, $\hat{\delta}(q_0, a) != \hat{\delta}(q_0, b)$ , 于是根据鸽笼原理, 这个DFA的状态也至少有 $2^n$ 个.

Q.E.D.

An Application Text Search

一些实际应用. 在实际的搜索引擎中, 大部分的场景下我们都不会使用状态机作为实际的搜索机制, 但是, 对于特定的场景下, DFA和NFA的应用是有可能的.
不过我们往往将Automata作为一个理论上的推导工具来使用, 所以在此跳过这个小结.

Finite Automata With Epsilon Transitions

此时, 我们对NFA进行延拓, 使得它能够接收空字符作为转移的信号
某种程度上, 可以将其理解为"在没有信号时, 也会自动地发生转移"的NFA

形式化地, 我们同样定义一个五元组

N = <Q, \Sigma, \delta, q_0, F>

此时几乎所有的定义都与NFA相同, 不同的是此处我们采用的转移函数的定义域为 $\Sigma \cup \epsilon$ , 即, 它可以接受空的字符作为转移信号.

Epsilon Closures

在完成了上面的定义之后, 我们同样地要对转移函数做延拓. 为了达到这个目的, 我们定义 Epsilon Closures的概念.
某种程度上, 它将"那些会自动地发生转移的区域"视为一个整体, 然后进行处理.

对于某个状态 $q$ , 它的 Epsilon Closures 是归纳定义的:

$q\in \text{ECLOSE} (q)$
$\text{ECLOSE} (q) = \text{ECLOSE} (q) \cup (\cup_{ p \in \text{ECLOSE} (q)} \delta(p, \epsilon))$

Extended Transitions and Languages for $\epsilon$ -NFA’s

根据上面的 $\epsilon$ -闭包定义, 我们自然地可以得出对于 $\epsilon$ -NFA的延拓转移函数. 它同样是归纳定义的:

$\hat{\delta}(q, \epsilon) = \text{ECLOSE} (q)$ ,
对于非空的字符串 $s := xa$ , 假定 $\hat{\delta}(q, x) =\{q_1,q_2, ..., q_k\}$ , 定义 $\hat{\delta}(q, s) = \text{ECLOSE}(\cup_{i}^{k} \delta(q_i, s))$

相当于, 每次转移完毕之后, 都要对转移的结果作一次闭包操作.
定义是非常自然的, 只是形式化表述花点功夫.

Eliminating $\epsilon$ -Transitions

对于这样添加了空字符的NFA, 同样的可以将其构造为一个等价的DFA.

具体而言, 大体上类似之前在NFA时所做的subset construction操作, 只是做了空字符串相关的闭包处理.
形式化地, 给出一个 $\epsilon$ -NFA: $E = (Q_E, \Sigma, \delta_E, q_0, F_E)$ , 我们构造一个对应的DFA:

D = (Q_D, \Sigma, \delta_D, q_D, F_D)

其中,

$Q_D$ : 仍然是原始NFA的状态子集的集合. 不同的是, $Q_D$ 中的每个元素都是一个 $\epsilon$ 闭包
$q_D = \text{ECLOSE}(q_0)$
$F_D = \{S| S \in Q_D, S\cap F_E \neq \emptyset\}$
$\delta_D(S, a) = \text{ECLOSE}(\cup_{q_i \in S} \delta_E(q_i, a))$

采用同样的思路, 通过定义一步步推导即可得到.

要证定理成立, 即证 $L(D) = L(E)$ .
要证集合相等, 需要从两方面证明. 我们要证明对于任意的字符串 $w\in (\Sigma \cup \epsilon) *$ , $w \in L(D)$ 等价于 $w \in L(E)$
即 $\hat{\delta_E} (q_0, w) \cup F_E \neq \emptyset$ 等价于 $\hat{\delta_D} (\text{ECLOSE}(q_0), w) \in F_D$