[CF记录] Round 975

2024-11-02

Note

记录CF竞赛的经历.

大概十天前第一次打了CF竞赛. 其实更早之前还打了ICPC的全球总决赛, 只不过太不正式了, 所以就暂且按下不表.
目前只参加了周期性的比赛, 也没有额外花时间在算法题上. 以后或许有机会刷刷算法题? 事情太多了…

总之, 目前的成绩如下:

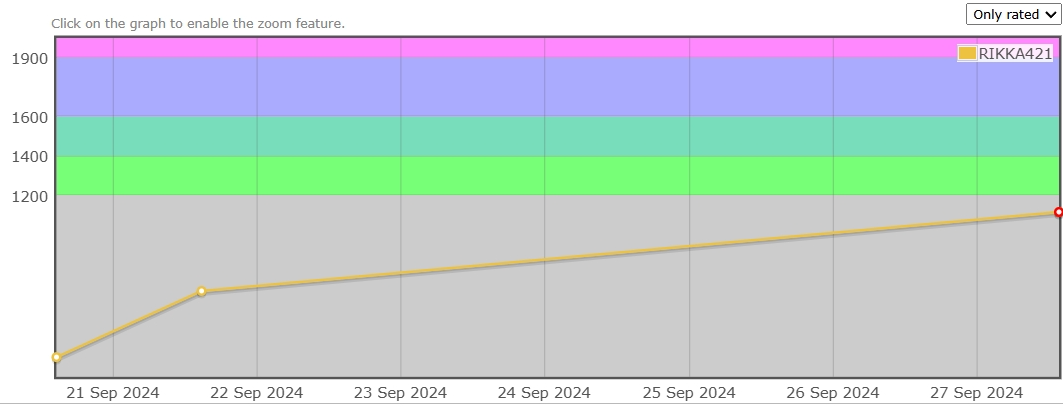
Round 975 - Div 2

往常的比赛都是在10点半左右开始, 打两个小时到两个半小时, 所以比赛结束的时候总是会到大概一点钟. 但是Round 975在9点45开始, 打2h30min刚好到12点左右, 对于CN玩家非常友好. 所以在没打之前就摩拳擦掌, 叫嚣着要AK之.
最终的成绩如下:

A max+size

将数列中的数染成红色, 要求:

染成红色的数不能相邻
最大化红色数中的最大值与数目之和, 即 $max(a_i) + size(a_i)$
输出那个最大值

容易证明, 对于size来说, 要么是总数的一半, 要么是一半加一(在总数为奇数的情况下).

且, $max(a_i)$ 的优化与 $size(a_i)$ 的优化几乎是不相干的.

所以, 我们总是会直接选取最大的那个数, 然后把接近一半的数选进来, 过程中处理一些细节即可. 总共的复杂度是 $O(n)$ 的

B 统计区间重叠数

给定n个端点, 它们会以全连接的方式, 构成 $n(n-1)/2$ 个区间.
给定一些数字k, 要求:

对于每个数字k, 给出"恰好被k个区间包含的点"的个数.

一开始没有想清楚, 只考虑了"区间端点"被区间覆盖的情况, 没有考虑区间内部点的情况. 同时, 在统计点所处在的区间数目的时候, 采用了类似" $(n-3) + (n-3)+(n-3)+(n-4)$ "的形式, 导致计算比较繁琐, 式子在直觉上的含义也不直观.

后面发现区间内部的点也需要考虑, 于是从头想了想, 很快发现了类似 $i * (n - i - 1) + (n+1)$ 的计算公式, 很显然, 也很直观. 于是顺势解决. 可惜还是花了很多时间.

总体的思路是分别用 $O(1)$ 的时间, 计算"区间端点"与"区间内点"的重叠区间数, 然后建立一个字典, 在k查询的时候输出即可.
计算的时间开销为 $O(n)$ , 空间开销在 $2n-1$ 的量级; 后续每次查询的开销都是接近 $O(1)$ 的(如果字典内部采用类似hash表的方式实现. )

C 把卡片放进抽屉

主要考察思维的题目.
给定一些卡片, 卡片上写着数字1-n, 每类卡牌数目不定.
给定k块钱, 最多可以购买k张卡片, 在n类卡片中购买. 买不买都行, 买哪种都行, 买多少都行, 只要不超过k张.
要求:

将原始卡片和购买后的卡片一同放进抽屉
每个抽屉放入卡片的数目必须相等(size)
每个抽屉中都不能有数字相同的卡牌(即, 同一个等价类的元素不能放进同一个集合)
给出所用抽屉的size的最大值

从极端情况开始考虑, 抽屉数值最大很明显是n(根据鸽笼原理), 最小明显是1(将每个卡片单独放在一个抽屉里)

再抛开k个硬币不管, 考虑卡片数目给定的情况. 经过思考可以发现, 抽屉的size可以为m, 仅当 $sum(a_i) \% m = 0$ , 且 $max(a_i) <= m$

那么接下来的思路就明确了: 对于某个给定的size, m, 以及当前的卡牌数目 $sum(a_i)$ , 考虑和 $sum(a_i)$ 最接近的数字 $M = m*int$ , 其中int是抽屉的个数. 当用那k个硬币把卡片总数补全到 $M$ , 且 $max(a_i)<int$ 时, size m是合法的.

再进一步考虑细节, 可以得到, 对于某个size = m, 我们考虑抽屉的个数int, 合法的int为 $max(max(a_i), sum(a_i) // m + 1)$ , 此时考虑卡片的总数能否被k"补全"即可. (此处考虑的是原始卡片数不能被m模的情况, 对于正好被m模的情况, int的值会稍有不同)

总之想清楚之后, 处理一些细节即可. 最终得到的形式是一个 $n$ 的遍历, 每个花费时间为 $O(1)$ , 总体时间是 $O(n)$ 的.

D 限定时间内征服城市

现在有n个城市, 每个城市给定了一个征服时限 $a_i$ , 要求

初始征服的城市可以自行选择
每回合, 选择当前相邻的城市之一进行征服(即, 选择左边或右边进行征服)
对于每个城市, 都需要满足征服时限
问, 能够完成合法征服的"登陆点"有几个

对于这个问题, 一开始的思路是, 首先将时限相同的城市"相连", 扩展为区间. 并将孤零零的城市视为单点区间. 由此, 我们讨论"征服时限"的等价类, 即一个个区间.
在这之后, 我们考虑区间 $[l, r]$ 的征服时限 $t$ , 将其变换为 $[r - t + 1, l + t - 1]$ . 它的含义是, “仅对于区间原始区间内的城市, 能够满足征服时限的合法登陆点的区间”. 只要在此区间内登录, 则原始区间的要求就可以被满足.

在这一步之后, 我考虑了将所有变化后的区间作交集操作, 并将结果作为最终的合法结果. 但是这一步是有问题的. 问题就在于, 我们不能孤立地考虑各个区间的"限制", 然后简单地将这些限制作交集操作, 而是需要联合考虑. 例如, 对于某个登陆点和某个城市, 达成要求需要我们一路向左扩张, 这实际上剥夺了我们向右扩张的可能.

明白这一点后, 我们进一步考虑, 即可得到限制区间的迭代式需求. 即, 将各个t排序, 然后从最近的那个ddl开始考虑, 慢慢向较宽松的ddl考虑. 这一点是必须的, 因为一旦不满足近的ddl, 问题就立刻终止了, 此时较远的ddl满不满足已经无关紧要.
具体而言, 我们先考虑最近的ddl $t$ , 得到对应的城市区间 $[l_1, r_1]$ 及其对应的合法区间, 然后, 对于下一个 $t_2$ 产生的城市区间 $[l_2, r_2]$ , 我们对其作合并操作, 得到 $[l_3, r_3] = [min(l_1, l_2), max(r_1, r_2)]$ . 它的含义是, 在 $t_2$ 时刻, 我们必须同时占领 $[l_1, r_1], [l_2, r_2]$ 两个区间, 也就等价于需要在此时刻占领 $[l_3, r_3]$ .
根据这个3号区间, 我们可以得到对应的合法区间. 此时再做交集操作.
之后一直做下去, 直到所有的期限被处理完毕即可.

对于算法占用的资源, 时间复杂度是 $O(n\log n)$ , 后面的计算和并集处理, 每个都是 $O(1)$ , 总和起来是 $O(n)$ 的. 对于空间复杂度, 我们在考虑等价区间的时候, 建立了一个时限与区间的对应字典, 字典的存储复杂度为 $O(n)$ , 每次访问的复杂度是 $O(1)$ 的

有趣的是, 我在问题的一开始就想到了要根据时限t做一个排序, 然后按序处理, 后来发现第一种想法是用不上排序的, 还以为做了无用功. 但是后面再一想, 发现排序在正确想法, 即第二个想法中是需要的. 也许这是看到与时限有关的问题, 大脑产生的直觉吧?

上面就是此次比赛的时候, 做出来的四道题.
总体而言, 在第二道题目上面花了太多的时间, 对于一开始那个复杂的计算思路花费了精力, 还编写了代码. 在接近1h时才开始写第三题. 如果在第二题节约20到30分钟, 是有可能把第五题也做出来的. 第五题看上去难度不大.
有趣的是, 我的排名周围的几乎所有选手都是"ABCE"的形式, 只有我做出来的是"ABCD". 也许这也算是第四题难度大于第五题的证明吧.

在把第四题代码交上去, 准备用剩下的几十分钟时间征战第五题的时候, 才发现第四题没过. 当时特别紧张, 深呼吸了好几次, 强制自己冷静下来, 考虑清楚问题的本质. 最终在时限前5分钟左右交上去过了. 后面即使面对简单的第五题, 无论如何也没有办法在五分钟内做出来了. 倘若在给我多10分钟, 甚至5分钟, 该有多好.

此外, 在本次比赛中我尝试使用了python的解题模版, 即建立一个solution类, 然后考虑它的solve方法, 并在诸如main和test之类的函数里进行调用. 后面实操下来, 发现不需要搞得那么复杂. 例如, 对于solve函数, 不用考虑其参数和返回值, 直接在内部进行input和print会方便很多. 此外, test函数的存在也是多余的, 不如直接采用"长文本注释存储样例 + 复制粘贴"的方式进行测试和调试.
其实, 最高效的方法是使用终端命令行对程序进行测试. 但是这么做有些繁琐, 而且对于不同输入格式的问题, 需要额外的更改命令… 我本来是想这么说的. 但是, 在实际尝试了之后, 我发现只需要把测试文本复制到test.txt中, 然后简单地运行如下命令即可

1	type test.txt \| python 01.py

这一套流程几乎没有需要改进的地方, 且效率很高, 比之前ctrl C ctrl V按来按去不知道简洁了多少.

看来在只有在踏出舒适圈之后, 你才会知道, “其实根本就没有什么锁链”.

总结完毕, 下面是赛后的一些思考. 对于后面的两道题, E题在看见的第一眼就感觉比较简单, 而且思路明确; F题在看见第一眼觉得它与打卡题"小改动, 大不同"的性质十分有趣. 在今天下午上课的时候思考了几十分钟, 也很快找到了思路.