[Algorithms] '少即是多': 只做需要做的事情_CN

尝试性地写了一篇算法相关文章.
一般而言我们会以"某种数据结构"或者"某道题目"作为中心来写东西, 但是这篇文章在包含几道题目的同时, 也并没有用到某个相同的结构 / 算法, 更多的是介绍了某种思维方式或者技巧?
总之, 大体上是一篇类似心得和感悟的东西, 暂且将其归为others类. 文章主要讲了"前-coding期"的内容, 即对问题进行建模, 思考大致思路的阶段. 将大致思路转换为伪代码, 再将伪代码实现为具体编程语言的过程, 在此不做过多涉及. 同时, 本文主要用中文书写, 英文版将作为TODO, 或许会有.

简述

开门见山地说, 这篇文章主要讲的是这样一个思路:

• 在面对问题A时, 对其进行基本的建模和分析, 得到一个朴素模型, 这一步往往是容易的.
• 根据模型, 得出一个更强的问题B, 使得在解决了B的情况下, A也会得到解决. 这一步也是容易的.
• 我们需要额外注意和分析的, 就是强问题B与弱问题A之间, 存在的"缝隙"或者"差距". 具体而言, 就是要考虑清楚有哪些信息是"B问题需要"而"A问题不关心"的. 这些差异性, 往往是进一步改进算法从而解决问题的关键.

Example 1: 中位数(vs排序)

让我们从一个简单浅显的例子开始说明.

问题描述:

给定n个整数 $[a_i]$ , 求出 $a_M$ , 使得 $a_M$为数列的中位数. 其中:

• 为了简化问题, 我们假设此时的n为奇数, 即 $n = 2k+1$
• 同时, 各个 $a_i$之间互不相等
• 假定我们要求, 需要以至多 $O(n)$的复杂度完成这件事

简单分析:

给定题面的情况下, 我们可以通过较为直接的思路, 得到一个更强的问题B.

具体而言, 在这个题目中, 我们很明显地可以看出:

• 对于中位数 $a_M$, 它是"处于中间的数"
• 形式化的, 对于 $a_M$, 它总是满足"存在k个数 $a_i$, 使得 $a_i < a_M$; 同时存在k个数 $a_j$, 使得 $a_j > a_M$"

那么, 我们可以很直接地得到一个朴素的暴力解法:

• 对给定的数列进行排序 ($O(n\log n)$)
• 对于排序后的数, 选择中间的 ($O(1)$)
• 总共开销为 $O(n\log n)$, 高于题目要求的 $O(n)$, 因此需要进一步优化

进一步分析:

在上面的朴素思路中, 我们将问题A:“求中位数"转换为了一个更强的问题B"排序”:

• 如果问题B可以用 $O(n)$求解, 那么皆大欢喜, 问题解决
• 如果不能, 就说明求解问题B的过程中, 我们一定"多做了些什么", 才导致复杂度"无谓的增加".
• 往往在考虑清楚"问题B比问题A多出来的一部分"之后, 我们就能得到符合要求的解法.

对于这个例子而言, 我们显然知道:

• 解决排序问题后, 我们得到了任意两个数 $a_i, a_j$之间的序关系. 得到的序关系合计为 $n(n-1)$对.
• 但是解决中位数问题后, 我们只得到了中位数 $a_M$与其他数 $a_i$之间的序关系. 得到的序关系为 $n-1$对, 对于其他数字之间的序关系我们并不关心.
• 换言之, 要解决中位数问题, 我们需要得到的信息是少于排序问题需要得到的信息的. 这就是所谓"强问题"与"弱问题"之间的"差距".

具体到算法上, 我们知道采用"二叉搜索树(BST)"的方法, 能够实现一个 $O(n\log n)$的排序算法; 而采用两个堆, 则可以实现一个 $O(n)$的求解中位数的算法. (关于堆算法的细节也挺有意思. 不过在别的博客中已稍有提及, 此次不做展开)
对于上述两个算法:

• 二叉搜索树的结构中, 保证了"左子节点 < 父节点 < 右子节点"的性质, 进而存储了任意两个节点之间的序关系
• 而在堆的结构中, 只保证了"父节点 > 子节点"的性质, 对于子节点间的序关系是不关心的. 因此, 存储的信息量与构建的开销都要少于二叉搜索树.

总而言之, 我们考虑清楚了"难问题B"比"简单问题A"之间的差距, 考虑清楚了B关心, 而A不关心的一些性质和信息后, 往往就能够对应的给出一个算法, 完成开销的优化.

Example 2: 因子分解(vs因子个数的奇偶性判断)

对于Example 1:“求中位数”, 由于它是一个被充分研究的问题, 所以我们当然很清楚的知道有一个 $O(n)$的算法, 所以也就看不出来"考虑清楚差距"和"给出优化算法"之间有什么关系. 事实上, 明白了"需要的序关系更少"和"给出堆相关的算法"之间, 确实有不小的gap.

但是, 对于下面这个问题, "考虑差距"对于我们优化算法思路的指导意义, 就体现的很充分了.

问题描述:

给定 $1, 2, 3, ..., n$共n个自然数, 我们假设每个数都代表了一个灯泡. 灯泡要么亮灯, 要么熄灭, 且初始都是亮灯状态. 下面, 我们遍历 $1-n$, 对于每个遍历到的 $i$, 做如下操作:

• 倘若 $j \% i = 0$, 那么所有 $j$上的灯泡状态翻转(即, 亮的灯泡熄灭, 灭的灯泡点亮), 其余灯泡不变
• 例如, 对于 $i = 3, n = 11$的情况, 那么 $j = 3, 6, 9$位置上的灯泡状态翻转, 其他灯泡不变.

下面, 我们给定一个数 $k$, 要求:

• 给出这样一个最小的n, 使得在 $1-n$共n个灯泡中, 亮的恰好有k盏
• 输出这个"尽可能小的"n

更加详细与精确的描述参见图片 (CodeForces, Round 976, Problem B) Problem - B - Codeforces.

简单分析:

!! NOTICE !!
在阅读下列分析前, 建议先对上面的问题进行初步的独立思考. 如此才能对下面的过程有切身的领悟与体会.

大致对于问题性质与数据量大小进行分析, 容易得到

• 这是一道与"素数", "因子"有关的一道数论方面的题目.
• 对于某个数字 $i$, $i$上的灯最后亮不亮, 只与其因子的个数 $f(i)$有关, 且更加具体地, 只与" $f(i)$的奇偶性"有关.
• 因此, 我们总要对"将某个整数分解为因子"这个过程进行探索.
• 问题的数据量为 $10^{18}$的量级, 因此$O(k)$的算法都是不可接受的, 我们必须找到 $o(k)$级别的算法, 例如 $O(\log k)$乃至 $O(1)$的算法.

根据上面的初步分析, 一个朴素的暴力想法是:

• 从1开始往后推, 对与每个数 $i$, 我们都对其进行因子分解
• 然后, 统计因子的个数, 并判断其奇偶, 从而得到 $i$上的灯泡是亮还是灭
• 一直这么做下去, 直到亮的灯泡总和达到 $k$
• 输出最小的n

显然, 上面的解法是强问题"因子分解"的解. 倘若这个解法的开销可以接受, 那么我们就自然地得到了弱问题"灯泡亮灭问题"的一个解法.
但是很遗憾, 简单的分析后我们可以得到, 这个暴力解法的开销是不可接受的:

• 一方面, 即使假设我们对于每个 $i$的分解, 都可以用 $O(1)$的时间来完成, 那么此时这个算法依然是 $O(n)$的.
• 而我们总是会有 $n>k$, 甚至可能会有n远大于k的情况发生(虽然我们之后会发现, n与k的数量级实际上是大致相等的), 因此这个算法也是 $O(k)$的.
• 另一方面, 我们显然知道, "因子的分解"不可能是个 $O(1)$的操作. 它本身的开销就是很高的.

因此, 朴素的暴力解宣告彻底失败. 我们需要寻求优化.

进一步分析:

进一步优化的思路是多种多样的:

• 也许考虑数论上的某些复杂公式, 直接给出n与k的闭式解, 然后通过 $O(1)$的方式直接给出?
• 也许通过分治法, 分别考虑 $1, n/2$与 $n/2, n$两段, 再不断二分, 从而引入一个 $O(\log n)$的算法?
• 也许考虑筛法和辗转相除法, 从前人的研究成果中获取灵感?

到底该怎么进行优化呢? 答案不是某些遥不可及的未知知识, 而就藏在我们思维的角落. 而"对于问题差距的分析", 就是找到这处宝藏的一把钥匙.

具体而言, 我们需要看清楚这一点:

• 暴力的解法中, 通过许多工作求出了任意数字 $i$的因子情况, 包括因子的个数与具体的数值
• 而在"灯光开灭问题"中, 我们只关心"因子个数", 且 只关心 “因子个数的奇偶性”. 这一点是需要格外强调的, 因为"求解因子个数"与"求解因子具体情况"几乎是个等价的问题, "奇偶性"才是画龙点睛的那一笔.
• 同时, 关心"因子个数的奇偶性"这件事, 也不等同于关心"一个数是素数还是合数". 因为我们知道, 一个素数的因子一定只有两个, 因此其因子个数一定为偶; 但是反之不然: 一个因子个数一定为偶的数, 可以是素数, 也可以是合数

所以, 我们可以总结如下: 我们关系的"灯泡开灭问题", 即A:“因子数奇偶问题”, 既不等价于B"具体因子情况", 也不等价于C"判断是素数还是合数". 后两个问题属于"更强的问题", 求解它们所必须的那些工作, 对于A来说可能是不必要的.
那么, A问题的等价问题究竟是什么呢? 答案是, “判断是否是平方数”.

具体而言:

• 对于给定的数字 $i$, 假设我们有分解式 $i = pq$ , 那么要么 $p, q$不相等, 因子成对增加 ($p, q$); 要么 $p= q =k$, 因子增加一个($k$)
• 考虑一番之后, 可以得到: 对于后面那种情况, $p= q =k$只会有一个解. 此时i是个平方数, 且因子个数为奇.
• 于是命题"i的因子个数为奇"与命题"i是一个平方数, 即存在k使得 $i = k^2$"是等价的
• 那么, 我们立刻得到结论: “灯泡只会在平方数所在的地方熄灭”
• 根据上面的结论, 考虑方程 $n^2 - n = k$, 那么很快得到一个 $O(\sqrt k)$ 的算法, 开销在 $10^9$的量级. (如果允许开平方的操作并将其视为常数时间开销, 那么 $O(1)$ 的算法也是存在的. )

自此, 通过"抓住问题本质", “削减求解多余信息而造成的不必要的开销”, 我们完成了算法的优化.

*背后的故事

可以看到, 只要考虑到"因子成对增加"与"因子单个增加"这件事与奇偶性的之间的关系, 问题的思路是一目了然, 水落石出的. 但是, 当我在CF赛场上实际遇到这题时, 思路却总是在素数分解的方向徘徊, 却总是不得要领, 找不到其中规律; 后来下了赛场补题, 也在二分法之类的死胡同里困顿良久.

最终, 我决定采用笨方法, 列出了前25个数的因子分解情况以及灯泡明灭的情况, 进行观察, 并惊讶地发现其满足

$$1, 2, 1, 4, 1, 6, 1, 8, 1, ...$$

的规律, 于是猜想其"作为等差数列, 前n项和为平方形式". 在沿着平方形式倒推之后, 才迅速地发现了个中规律, 水到渠成一般证明了"平方数灯灭"的正确性.

在揭开面纱反推原理后, 我不得不惊叹数学的玄妙: 想明白之前, 怎么也找不出规律; 想明白之后, 却发现规律简单的惊人. 可谓是"天国藏在鼻尖之下".

因此, 对于这一题而言, "抓住问题本质来分析"的方法, 其实也是马后炮的说辞. 毕竟真正的思考过程是依靠罗列前几项, 从特解到通解的方式来实现的. 不过这种时候的分析, 应该也多少能够带来一些帮助吧.

Example 3: 前n项和奇偶性判断(vs前n项和)

前面的Example 1太浅显, 几乎没有什么分析的机会; Example 2则有些太难(至少对我而言), 所以分析了也没有多大用处. 此处的Example 3作为div3的problem B, 或许处于中等位置. 因此在此也罗列出来, 作为补充.

题目描述:

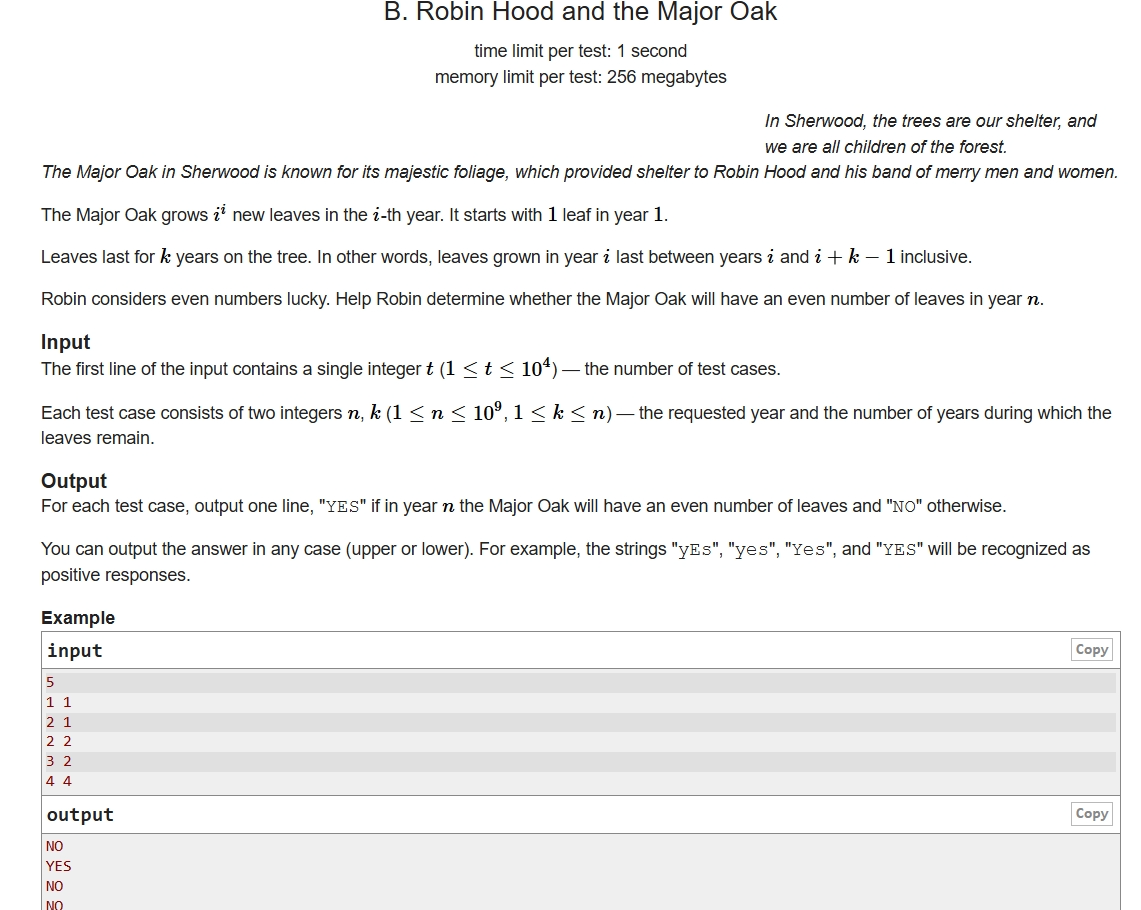
对于一棵树, 它每天会生长一些叶子, 叶子存活若干天后会掉下. 其中的规律为

• 第 $i$天, 会长出 $i^i$片叶子
• 叶子存活k天后, 会凋落

现在给定数字n, 要求得到第n天, 树上叶子数目的奇偶性.

更加详细与精确的描述参见链接 (CodeForces, Round 974, Problem B) Problem - B - Codeforces

简单分析:

由于此题的题解已经在
[CF记录] Round 973 && 974 | RIKKA’s Blog (rikka421.github.io)
中给出, 此次便只做简要分析.

通过思考, 我们容易发现

• 给定数列"每天生长的叶子数", $a_i = i^i$
• 对于第n天, 树上存在的叶子数其实是数列 $a_i$的后 $k$项和 $T_k$
• 对于后k项和, 可以通过前n项和 $S_n$给出: $T_k = S_{n} - S_{n - k}$

那么, 朴素的暴力想法当然是直接做次方运算, 然后做求和操作. 但是由于k的量级在 $10^9$, 因此不论是运算开销还是溢出的处理都是不可接受的.

进一步分析:

进一步的分析可以得到: 我们其实并不关心具体的前n项和 $S_n$的数值, 而只关心 $S_n$的奇偶性. 而奇偶性经过研究之后, 就可以迅速发现其具有周期的性质, 于是很快得到一个 $O(1)$的闭式解.

在此例中, 我们的"强问题"就是"求 $i^i$的前n项和", 而弱问题是"给出前n项和的奇偶性". 显然, "求和"这件事需要求解的信息量是远大于"求奇偶性"的, 因此, 在只考虑奇偶性的性质后, 开销就迅速地降到了 $O(1)$. 这就是"不求解多余信息, 只求解必要信息"带来的好处.

常见应用场景

1. 朴素的暴力解法容易构建: 例如E.1中, 为了求中位数而给出的排序解法
2. 信息量过多 / 信息冗余的模型能够给出: 例如E.2中, 给出的因式分解的模型. 对于求解原问题, "进行因式分解"的操作其实得到的是过多的信息量, 许多"因子的具体值"这样的信息对于求解原问题来说是多余的.
3. 朴素暴力解 / 冗余模型的性质是比较清楚的: 例如, 对于排序算法的复杂度我们了如指掌, 对于素数因式分解的算法和复杂度我们也能够大致预估

对于某些问题, 简单地分析无法让我们构建出一个大致的模型, 或者得到一个朴素的暴力解; 而当把问题分析透彻时, 算法就已经自然给出, 不需要经历"从朴素解进行优化"的过程. 对于这些问题, 本篇文章中"少即是多""去芜存菁"的思路就没什么作用.

总结

正如我开头所说的, 这篇文章大体上是一篇类似心得和感悟的东西. 写作的动机其实就是发现976-B题解法时, 大彻大悟的醍醐灌顶感. 之后就顺着这种"抓住主要需要求解的信息, 抛开不关心的信息"的思路, 大致归纳了几题类似的题目.

其实, 对于ICPC2024 World-Final中的赛马一题, 也有点类似的感觉. 具体讲清楚思考的过程以及对于朴素算法的复杂度分析比较费劲, 所以就没有作为例子, 只是在这提一嘴. 总之, 我看见那题第一眼, 朴素的想法是用图来做, 并讨论图的连通性. 进一步思考后, 发现图的解法复杂度是不可接受的. 后面细细想来, 就是因为归约成的图问题(假设为问题B)“太强大了”.
具体地说, 赛马问题(假设问题A)实际上是问题B的一个特解或者说弱形式. 假设问题B有复杂度 $n \log n$的解法, 那么已经给出了A的一个解, 复杂度就不会超过 $n \log n$ , 反之, 假设问题B没有复杂度 $n \log n$的解法, 那么说明不了任何问题, 我们还是得单独地讨论A.
更形式化的语言涉及到计算理论方面, $P, NP$ 之类的形式化定义, 要说清楚不太容易, 所以在此只做一个直觉的介绍.

言归正传, 本文的形式化理论语言, 其实就是计算理论里, 与问题归约有关的内容. 文章只是进一步地结合例子, 强调在思考实际问题时要牢记"去芜存菁", 从而做到能从一个朴素构建的暴力模型出发, 推导出能够满足实际要求的高效模型. 也许能够作为无从下手时, 确定思路的一个指导.

以上.

(2024-10-02 编写大致用时3h)