LearnLog

基于上海交通大学强化学习课程系列课程学习RL的笔记.
SJTU RL Course (wnzhang.net)

此为第一讲的内容, 主要对RL做了导论的内容, 同时以多臂老虎机作为例子, 讲述了探索与利用相关的内容.

系列课程的大体结构如下:

主要内容

  • 面向决策任务的人工智能
  • 强化学习的基础概念和研究前沿
  • 强化学习的落地现状与挑战

面向决策任务的人工智能

两种人工智能任务类型

大体上, 可以将人工智能任务分为两类: 预测型任务和决策型任务

预测型任务: 包含有监督学习和无监督学习

  • 根据数据预测所需输出（有监督学习）
  • 生成数据实例（无监督学习）

决策型任务: 在动态环境中采取动作（强化学习）

  • 转变到新的状态
  • 获得即时奖励
  • 随着时间的推移最大化累计奖励
  • Learning from interaction in a trial-and-error manner

其中, 两者最大的差别就是, 在决策任务中引入了环境与行动的概念, 即:

  • 算法给出的结果是作为一个决策被执行的, 它会与环境进行交互, 并对智能体接下来的行为产生影响
  • 而在预测型任务中, 算法给出的结果实际上并不产生什么影响. 人们用不用, 怎么用这个结果, 与算法的执行并不相干.

决策智能的任务与技术分类

根据决策环境的性质, 可将决策任务大致分为四类:

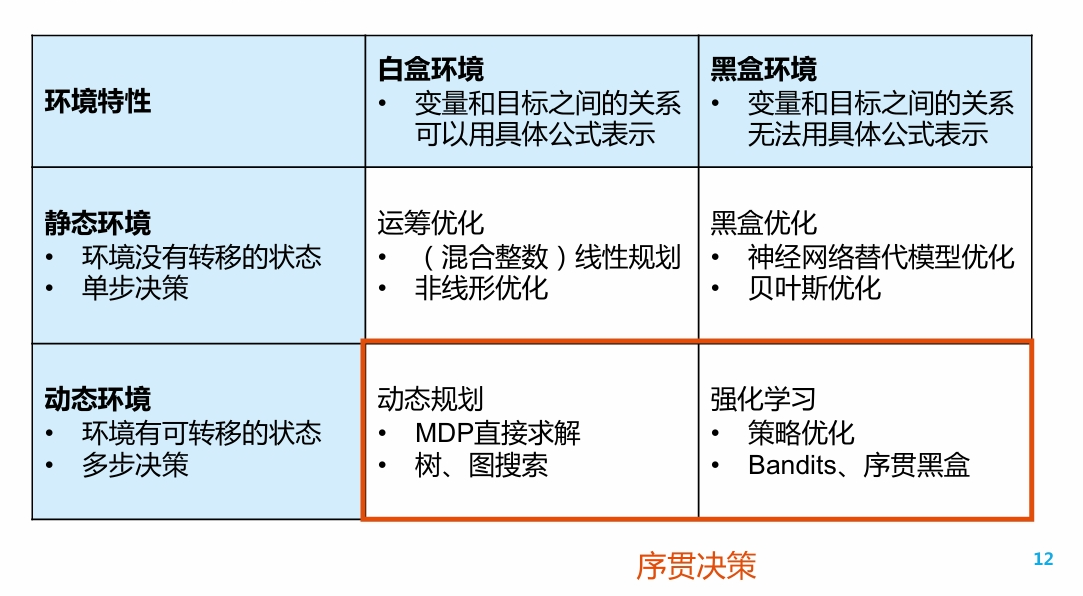
其中, 对于"白盒环境"中的问题, 即变量与优化目标间的关系可用数学公式具体表述的问题, 我们一般不将其作为RL问题考虑, 而是将其看做优化问题或动态规划问题.

对于动态环境中的问题, 我们将其作为"序贯决策"Sequential Decision Making来考虑.

绝大多数序贯决策问题，可以用强化学习来解

强化学习的基础概念与研究前沿

基础概念

对于强化学习过程的每个时刻, 都可以采用三元组

<Ot,At,Rt><O_t, A_t, R_t>

来描述. 其中OO代表观测, AA代表动作, RR代表奖励

历史（History）:

  • 观察, 动作和奖励的序列.
  • Ht=O1,R1,A1,O2,R2,A2,...,Ot,RtH_t = O_1, R_1, A_1, O_2, R_2, A_2, ..., O_t, R_t

状态（state）

  • 用于预测的信息, 注意和"观测OO"相区分
  • 是关于历史的函数: St=f(Ht)S_t = f(H_t)

策略（Policy）

  • 学习智能体在特定时间下的动作方式, 是状态到动作的映射
  • 确定性策略（Deterministic Policy）: a=π(s)a = \pi(s)
  • 随机策略（Stochastic Policy）: π(a∣s)=P(At=a∣St=s)\pi(a|s) = P(A_t = a| S_t = s)

奖励（Reward）

  • 一个定义强化学习目标的标量, 用于判断"什么是好的"
  • 将状态 / <状态, 动作>映射到一个标量上: RtR_t或者r(s,a)r(s, a)

环境的模型（Model）

  • 用于模拟环境的行为
  • 预测下一个状态: Pass′=P[St+1=s′∣St=s,At=a]\mathcal{P}_{a}^{s s'} = P[S_{t+1} = s' | S_t = s, A_t = a]
  • 预测下一个立即奖励: Ras=E[Rt+1∣St=s,At=a]\mathcal{R}_{a}^{s} = E[R_{t+1}| S_t = s, A_t = a]

学习目标:

  • 在与环境持续交互的过程中, 最大化期望累计奖励总和
  • 即maxπ Eπ,Env[R0+λR1+...]max_{\pi}\ E_{\pi, Env} [R_0 + \lambda R_1 + ...]
  • 其中, RiR_i是随机变量, 其概率分布与π\pi和EnvEnv有关

定义策略的价值函数:

  • 价值是一个标量, 用于定义对于长期来说什么是"好"的
  • Qπ(s,a)=E[r(s0)+λr(s1)+...∣s0=s,a0=a,π]Q_{\pi}(s, a) = E[r(s_0) + \lambda r(s_1) + ... |s_0 = s, a_0 = a, \pi]
  • Bellman等式: Qπ(s,a)=r(s)+λ∑s′∈SPsa(s′)∑a′∈Aπ(a′∣s′)Q(s′,a′)Q_{\pi}(s, a) = r(s) + \lambda \sum_{s' \in S} P_{sa}(s') \sum_{a' \in A} \pi (a'|s')Q(s', a')
  • 其中, si,ais_i, a_i分别是状态和动作的随机变量, QπQ_{\pi}则求解了一个条件期望
  • Bellman等式可以根据定义以及环境的马尔科夫性质导出.

强化学习的方法分类:

  • 基于价值: 根据价值函数对策略进行更新. 策略是隐含的
  • 基于策略: 基于策略进行更新. 没有价值函数
  • Actor-Critic: 学生听老师的. 有策略, 也有价值函数

研究前沿

深度强化学习

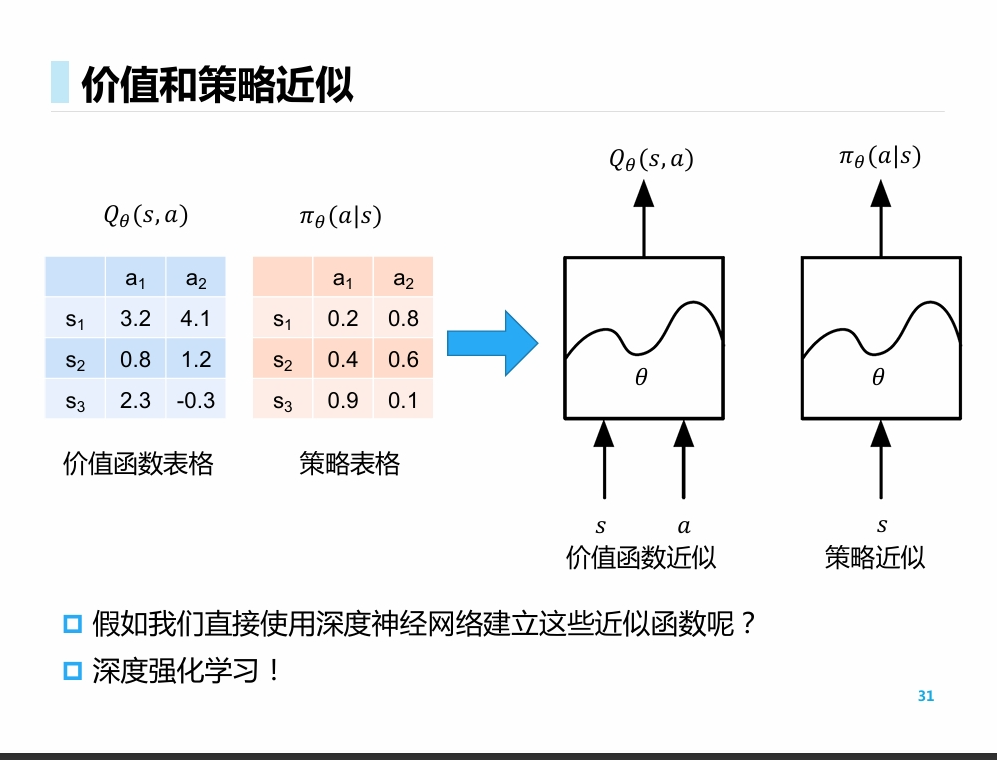
  • 在前面的例子中, 我们使用表格来描述价值函数和策略表格.
  • 而很多情况下, 离散化的表格无法对价值与策略进行描述
  • 因此, 我们选择引入神经网络, 对其进行近似

2012年AlexNet在ImageNet比赛中大幅度领先对手获得冠军
2013年12月, 第一篇深度强化学习论文

Volodymyr Mnih, Koray Kavukcuoglu, David Silver et al. Playing Atari with Deep Reinforcement Learning. NIPS 2013 workshop.

  • 深度强化学习是一种端到端的方法.
  • 它使得传统方法中的许多特征提取工程变得不必要
  • 从而使强化学习从实验室中的学术技术变成可应用到工业界的工程技术

探索与利用

探索还是利用? 这是序列决策任务中的一个基本问题.

策略探索的一些原则:

  • 朴素方法 Native Exploration: 添加策略噪声 ϵ\epsilon-greedy
  • 积极初始化 Optimistic Initialization
  • 基于不确定性的度量 Uncertainty Measurement: 倾向于尝试那些具有不确定性收益的策略
  • 概率匹配 Probability Matching

多臂老虎机 multi-armed bandit:

  • <A,R><\mathcal{A}, \mathcal{R}>
  • A={a1,a2,...,ak}\mathcal{A} = \{a_1, a_2, ..., a_k\}
  • R(r∣ai)=P(r∣ai)\mathcal{R}(r|a_i) = P(r|a_i)

算法描述:

考虑Regret函数:

  • 决策的期望收益: Q(ai)=Er∼P(r∣ai)[r]Q(a^i) = E_{r \sim P(r|a^i)}[r]
  • 最优决策: Q∗=max⁡ai∈AQ(ai)Q^* = \max_{a^i \in \mathcal{A}} Q(a^i)
  • 收益差: R(ai)=Q∗−Q(ai)R(a_i) = Q^* - Q(a^i)
  • Regret: σR=Ea∼πΣt=1TR(ati)\sigma_R = E_{a \sim \pi} \Sigma _{t = 1}^{T} R(a_t^i)

显然, 使Regret最小化的策略, 与使收益最大化的策略是等价的.

考虑两个最简单的情况:

  • 一直探索新决策(例如, 等可能选择所有动作): σR∼T\sigma_R \sim T
  • 一直不探索新决策(例如, 在T次动作后, 只选择当前最优动作): σR∼T\sigma_R \sim T
  • 两种情况下, Regret都会线性增长, 无法收敛.

具体而言, 对于每个机械臂, 考虑其服从0/1分布. 那么对其进行n次采样得到的均值ee, e是一个服从多项分布的变量.
考虑此时得到的"最好选择", 满足均值最大的性质. 它也是一个随机变量.
此时, 倘若其余机械臂的取值都小于目前这个最好选择的"实际值", 那么Regret就会线性增长.
因此求期望之后, Regret也会线性增长.
TODO: 用概率论的语言, 仔细探究其分布关系.

问题的下界:

σR=Ω(log⁡T)\sigma_R = \Omega(\log T)

Lai, Tze Leung, and Herbert Robbins. “Asymptotically efficient adaptive allocation rules.” Advances in applied mathematics 6.1 (1985): 4-22.

因此, 我们希望能够寻找到一个对数增长的, 或者至少是次线性增长的策略. (至少要使"懊悔增长速度"不是恒等值)

贪心策略和ϵ\epsilon-greedy策略

  • 对于总选择当前最优解的贪心策略, 其Regret增长速度是线性的.

  • 对于以常数ϵ\epsilon进行探索的ϵ\epsilon-greedy策略, 其增长速度小于贪心, 但仍然是线性的.

  • 对于随时间衰减的ϵ\epsilon-greedy策略, 理论上是次线性的, 只是我们很难找到一个理想的衰减规划.

    某种程度上, 后面提到的其他策略, 都是显式给定ϵ\epsilon衰减方式的ϵ\epsilon贪心. (暴论)

乐观初始化

  • 给定Q(ai)Q(a_i)一个过高的初始化值, 然后采用贪心, 从而鼓励探索的行为.
  • 起始是一个有偏估计，但是随着采样增加，这个偏差带来的影响会越来越小
  • 仍然可能陷入局部最优 (给定初始值越高, 陷入最优的可能性越小, 但是无法避免)
  • 从极限考虑, 依然是线性的

显示考虑动作的价值分布

基于不确定性的度量

根据Hoeffding 不等式, 我们有

P[E[x]>xtˉ+u]≤e−2tu2,x∈[0,1]P[E[x] > \bar{x_t} + u ]\leq e^{-2tu^2}, x\in [0, 1]

于是, 在给定一个 p=e−2tu2p = e^{-2tu^2}, 如 p=0.9p = 0.9的情况下, 我们可以根据tt解出uu的值. 从而导出这样一个策略:

a=arg⁡max⁡ai∈AQt^(ai)+Ut^(ai)a = \arg \max_{a^i \in \mathcal{A}} \hat{Q_t}(a^i) + \hat{U_t}(a_i)

其中

Ut^=−log⁡p2Nt(a)\hat{U_t} = \sqrt{-\frac{\log p}{2 N_t(a)}}

收敛性: 对数收敛

lim⁡t→∞σR≤8log⁡t  Σa∣△a>0△a\lim_{t \rightarrow \infty } \sigma_R \leq 8\log t \ \ \Sigma_{a | \triangle a > 0} \triangle a

Hoeffding, Wassily. “Probability inequalities for sums of bounded random variables.” The Collected Works of Wassily Hoeffding. Springer, New York, NY, 1994. 409-426.

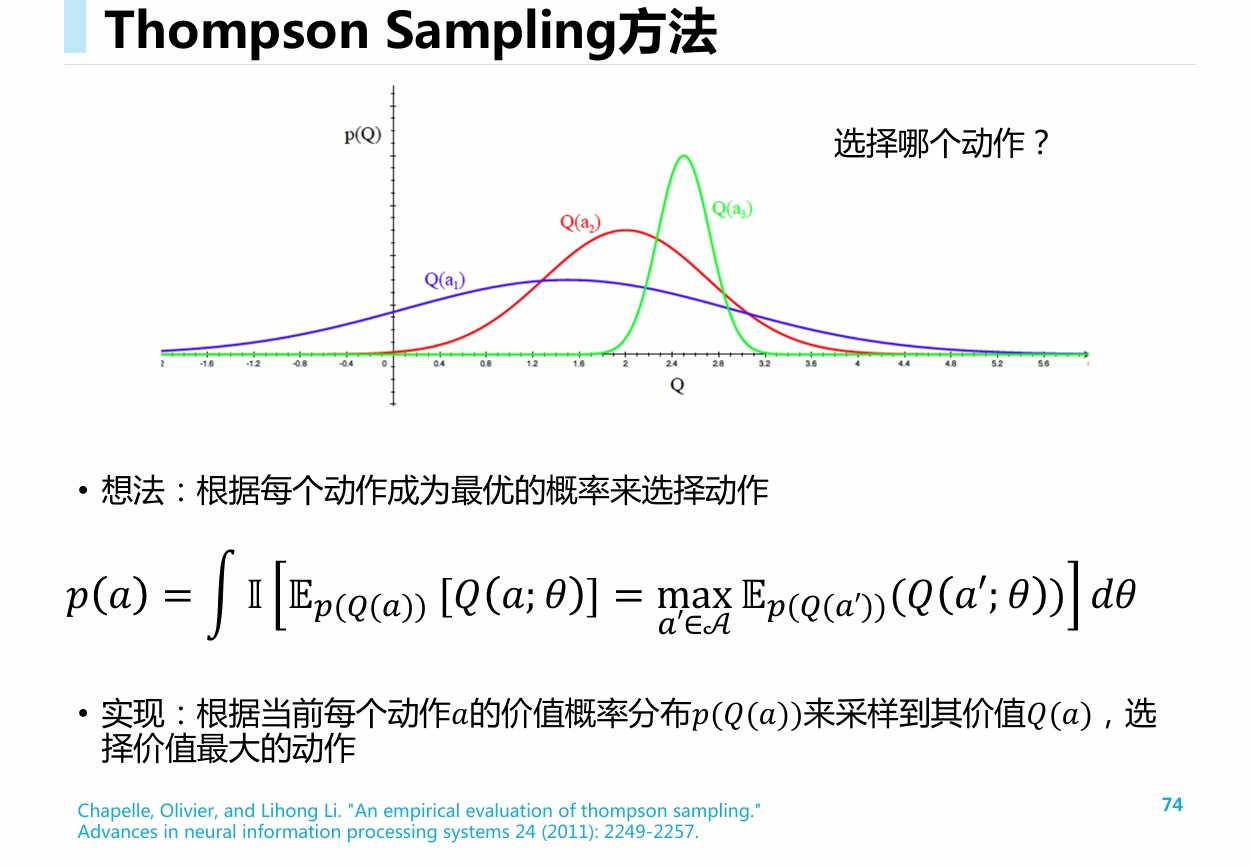
Thompson Sampling方法

  • 对于每个动作的期望汇报rr的概率分布做建模, 例如, 使用beta分布建模
  • 根据每个动作的分布进行采样, 对于采样得到的结果, 直接排序
  • 选择最优动作执行, 更新该动作的分布

Chapelle, Olivier, and Lihong Li. “An empirical evaluation of thompson sampling.” Advances in neural information processing systems 24 (2011): 2249-2257.

总结

  • 探索与利用是强化学习的trial-and-error中的必备技术
  • 多臂老虎机可以被看成是无状态(state-less)强化学习
  • 多臂老虎机是研究探索与利用技术理论的最佳环境
  • 理论的渐近最优regret为𝑂(log𝑇)
  • ε-greedy、UCB和Thompson Sampling方法在多臂老虎机任务中十分常用，在强化学习的探索中用也十分常用，最常见的是ε-greedy

*感想

ε-greedy的方法在极限分析上并不是最优的, 但是实践中最长应用, 这可能是由于它易于实现, 同时能够适应多种不同的分布场景. 实践上最优和理论上最优产生了一点点的gap, 有趣.

(2024-10-07 大致编写用时2h)

backtop