[CF记录] VP Round 969

Round 969的VP. 由于前两题之前都已经听过了, 所以做的很快. 最终的成绩是4题左右.

---

Round 973 - Div 2

最终的成绩如下:

挺可惜的. 要是之前把树研究过了, E题说不定就能做出来了.

A Dora’s Set

题意：在$[l, r]$中选出$3k$个不同的正整数数并分成$k$组，每组三个正整数必须两两互质。求$k$的最大 值。

简单分析

注意到以下事实:

• 对于奇数$a$, 容易证明$(a, a+1, a+2)$是两两互质的.
• 对于任意两两互质的三元组, 内部至少含有两个奇数.
• 因此, 选出"连续三个数"就是最高效的做法.

code

print( ((r + 1) // 2 - l // 2) // 2)

其中, 内部的整除号保证了奇偶数的性质; 外部的整除号保证了"4个数为一个单元"的性质.

B Dora’s Set

题意：对于给定的$[a_i]$, 我们做如下的操作:

• + / - l r. 表示对于任意$a_i \in [l, r]$, 进行++或--操作
  考虑一系列操作之后, 得到的结果数列的最大值.

简单分析

注意到以下事实:

• 对于原数组的最大值$m$, 无论怎么进行操作, 得到的$m'$依然是新数组的最大值.

因此, 先记录原数组的最大值, 再记录对其进行的操作即可.

复杂度是$O(n)$的

Dora and C++

题意：给定一个序列，你可以任意次单点$+A$或$+B$，最小化极差。

简单分析

注意到如下事实:

1. 由于进行操作的次数是任意的, 且我们只关心序列的极差, 所以这个问题明显与模和等价类有关.
2. 对于操作数$op = [A, B]$, 得到的极差与操作数$op = [A, B, |A - B|]$是等价的.
3. 对于操作数$op = [A, B]$, 得到的极差与操作数$op = [gcd(A, B)]$是等价的.
4. 对于序列$[a_i]$和操作数$op = [A,B]$, 令$d = gcd(A,B)$我们做操作$[a_i \% d]$. 然后, 对这个新数列进行考虑即可.

对于事实2, 容易从例子中发现; 对于事实3, 可以从例子中得到直观上的猜想. 形式化的证明将在下面给出.

根据事实3, 我们容易发现, 不断进行操作以最小化极差, 其本质是将$[a_i]$数组化为模$d$同余的等价类, 然后投射到一个环上, 之后考虑环上数与数之间的最小间距即可. (事实4就是在做这一件事. )

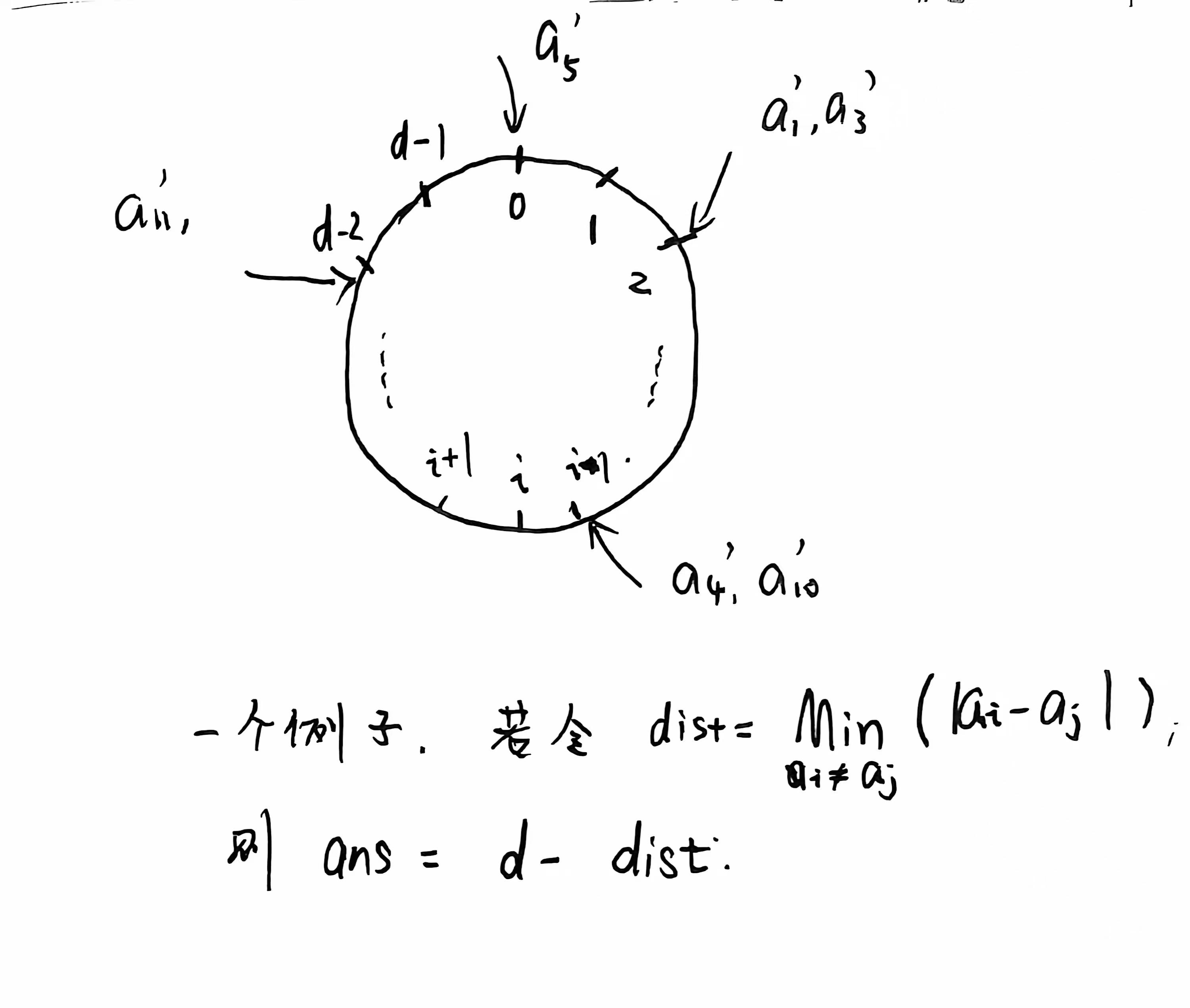
Code

import math
 
T = int(input())
for _ in range(T) :
	n, a, b = map(int, input().split())
	d = math.gcd(a, b)
	a = list(map(int, input().split()))
	a = [x % d for x in a]
	a.sort()
	res = a[n - 1] - a[0]
	for i in range(1, n) :
		res = min(res, a[i - 1] + d - a[i])
	print(res)

形式化证明

我们要证的事情实际上已经有了一个名字: Bezout’s Identity, 以下是它的维基百科.
Bézout’s identity - Wikipedia

下面用自己的语言将维基百科上的证明过程进行叙述.

事实上, 在没有看维基百科的情况下, 我是将其转换为了一个等价命题进行证明的:

• 考虑$\{ax + by | ax + by > 0, x, y\in Z\}$. 其中$a, b$互素. 证明该集合中的最小值$d$为1. (该集合显然非空. 最小元素的存在性由良序公理保证)

容易发现, 上面的新命题和我们的原命题是等价的.