LearnLog

基于上海交通大学强化学习课程系列课程学习RL的笔记.
SJTU RL Course (wnzhang.net)

此为第二讲的内容, 主要讲述了马尔科夫决策过程MDP的概念, 并给出了策略度量, 策略值函数, 基于值函数进行策略提升的内容.

MDP

!!Attention!!
在下面的描述中, 我们会用大写字母来表示随机变量, 使用小写字母来表示随机变量的具体取值
如使用StS_t来表示随机变量"t时刻的状态", 而用sts_t来表示t时刻所取到的具体状态.
同时, 在取期望时, 若不加说明, 则是对方括号内的随机变量取期望.

随机现象与随机过程

对于世界中的各种随机现象, 我们可以用概率论的方法对其进行建模, 如用随机变量 / 随机向量对某个随机事件进行描述等.

  • 用伯努利分布描述硬币的正反面
  • 用多项分布描述多次投掷硬币后, 正面朝上的硬币数量
  • 用高斯分布来描述许多的物理现象

对于随机现象的描述能够帮助我们解决一些问题, 但是在某些场景下, 我们会将一系列随机事件整体性地考虑, 将它们视为"随机过程", 并用

P(St+1∣S1,S2,...,St)P(S_{t+1} | S_1, S_2, ..., S_t)

来描述它们.

  • 例如: 天气的变化, 足球比赛, 生态系统的演进等.
  • 这些过程中, 我们认为某个时刻的状态分布, 会受到历史状态的影响.

随机过程是一个或多个事件、随机系统或者随机现象随时间发生演变的过程

  • 概率论研究静态随机现象的统计规律
  • 随机过程研究动态随机现象的统计规律

* 一些发散

  • 随机过程的建模包含的理念是: 我们假定在给定历史状态的前提下, 下一个状态的概率分布是确定不变的.
  • 我们可以考虑"决定论"观点的建模, 来描述一个"确定性过程", 即在给定所有历史状态的前提下, 下一个状态是确定性的. 此时, 形式化的, 这个过程可以通过映射f(S1,S2,...,St)=St+1f(S_1, S_2, ..., S_t) = S_{t+1}来描述. 相比于"随机过程"的建模, 这是一个更强的假设.
  • 同样的, 我们可以考虑描述一个"强随机过程". 这时我们假定, 给定所有历史状态的前提下, 当前状态的分布的分布是确定的. 显然, 此时给定的是一个更弱的假设, 建立的是更加复杂的模型, 描述起来也更加复杂.
  • 当然, 我们也可以假定一个更复杂的图景: 即, 不仅当前状态的分布是不确定的, 而且当前状态的分布的分布也是不确定的. 这个过程可以一直进行下去, 没完没了.
  • 真正的物理世界究竟服从怎么样的模型呢? 我不得而知. 但是, 这些模型对于解决某些具体问题而言是很有用的.

总而言之, 对于"随机过程"的建模已经有些过于强大, 也过于复杂了. 因而我们往往做出妥协, 考虑弱一些的特殊形式, 即马尔科夫过程

马尔科夫过程 Markov Process MP

对于某些特殊的随机过程, 即马尔科夫过程, 我们假定

  • 状态从历史（history）中捕获了所有相关信息
  • 当状态已知的时候，可以抛开历史不管
  • 也就是说，当前状态是未来的充分统计量

此时, 我们有

P(St+1∣St)=P(St+1∣S1,S2,...,St)P(S_{t+1}|S_t) = P(S_{t+1} | S_1, S_2, ..., S_t)

显然, 虽然MP过程中状态的转移可以无穷无尽地进行下去, 但是在给定了一个MP之后, 每个状态的概率分布都是确定的, 换言之, 给定MP后, 就相当于给定了一系列随机变量StS_t的分布.
理论上, 我们可以任意地给出P(St=s)P(S_t = s)的具体分布. 但是在实际中, 对于稍微复杂一些的MP, 这个具体分布往往就处于黑箱状态.

马尔科夫过程 Markov Reward Process MRP

  • 在马尔可夫过程的基础上加入奖励函数和折扣因子，就可以得到马尔可夫奖励过程（Markov reward process）
  • 相比于马尔科夫过程, MRP在每个状态都会有一个对应的奖励rr, 其随机变量记为 RtR_t. 显然, 它可以通过 StS_t和 r(s)r(s)来导出, 即 Rt=r(St)R_t = r(S_t)

对于某个的状态序列St,St+1,...S_t, S_{t+1}, ..., 我们定义该序列的回报为

Gt=Rt+γRt+1+...=∑k=0∞γtRt+kG_t = R_t + \gamma R_{t+1} + ... = \sum_{k = 0}^{\infty} \gamma ^{t}R_{t+k}

显然

  • 定义的 GtG_t是一个与序列相关的随机变量.
  • 在给定了一个MRP的情况下, 其任意时刻的回报 GtG_t的分布是确定的, 期望奖励 G=E[G0]G = E[G_0]也是确定的.

序列回报的形式

上述等比衰减的回报形式有什么好处呢? 大致可以分为两个方面

  1. 一定程度上保证了总体回报值 GtG_t的收敛性
  2. 保证了 GtG_t具有序关系上的良好性质

对于收敛性,

  • 让我们假设当前还没有确定序列回报是按照上述过程进行衰减的.
  • 此时, 对于某个序列 St,St+1,...S_t, S_{t+1}, ..., 我们有一个回报序列 Rt,Rt+1,...R_t, R_{t+1}, ....
  • 那么, 我们就要考虑给出一个对应的实数随机变量 RR, 用它来整体性的描述上述序列的"好坏"

我们可以发现如下的事实

  • 对于MP过程, 即使它是一个无穷的过程, 由概率的性质也可以天然地保证最终的概率分布 P(St)P(S_t)是收敛的
  • 但是对于MRP过程, 最终得到的"总体回报" RR却不一定是收敛的. 例如, 我们考虑对回报序列进行简单求和操作. 那么, 倘若 Ri=MR_i = M恒成立, 在 T=∞T = \infty时总回报就趋于无穷.
  • 此时, 若我们考虑有限状态的MRP, 同时考虑等比衰减的求和形式, 此时得到的 ∑k=0∞γtRt+k\sum_{k = 0}^{\infty} \gamma ^{t}R_{t+k}就是收敛的了.

进一步考虑之后, 我们发现:

  • 对于给定序列[R1],[R2][R_1], [R_2], 实际上我们并不关心具体得到的 R1,R2R^1, R^2的值
  • 相反, 我们关心的是 R1,R2R^1, R^2之间的大小关系. 因为我们实际上是想要凭借大小关系, 来比较两个序列之间的好坏
  • 因此, 比起考虑具体数值的性质, 我们更多地考虑它确定的序关系所具有的性质.

对于序关系, 我们给出如下定理:

TODO: 为何选定线性形式呢? 这一点没太想明白, 还需要进一步考虑.

马尔可夫决策过程 Markov Decision Process MDP

  • 给定一个MRP, 我们将其作为环境的建模
  • 同时, 我们加入策略的建模. 此时环境状态的转移不再完全取决于环境, 而有部分取决于决策者的动作
  • 即, P[St+1∣St,At]P[S_{t+1} | S_t, A_t]

MDP形式化地描述了一种强化学习的环境

  • 环境具备完全的可观测性
  • 即, 当前状态可以完全表征过程, 下一个状态可以完全地由当前的状态决定（马尔可夫性质）

* 在某些时候, 下一个观测量Ot+1O_{t+1}不一定由之前的观察量OtO_{t}来决定. 但是别忘了, "状态 SS"与"观测 OO"并不等同. 状态可以是历史观测序列和动作序列进行复杂的作用而得出的结果.
因此, 对于很多的过程, 我们都可以假定其具有状态的马尔科夫性质, 此时观测的马尔科夫性质往往不必满足

形式化地, 对于一个MDP, 我们如下五元组进行描述

<S,A,Psa,γ,r><S, A, P_{sa}, \gamma, r>

  • SS: 状态集合
  • AA: 动作集合
  • PsaP_{sa}: 状态转移概率, 也作 P(⋅∣s,a)P(\cdot|s, a)
  • γ∈[0,1]\gamma \in [0, 1]: 对未来奖励的折扣因子
  • r:S×A→Rr: S \times A \rightarrow R: 奖励函数

* 此时我们考虑的奖励函数是一个确定性的映射; 对于某些情况, 奖励函数也可以服从一个分布. 此时我们往往考虑当前期望. 例如对于多臂老虎机的奖励建模就是这种情况.

  • 对于一个给定的MDP和给定的策略π(a∣s)\pi(a|s), 所有的随机变量的分布也是完全确定的.
  • 我们可以通过从初始状态开始, 不断进行转移复合, 来求解所需要求解的随机变量
  • 但是实践当中, 由于状态转移过于复杂, MDP过程具体分布往往不可见, 处于黑箱状态

RL vs ML

对于传统的ML(SL, UL),

  • 我们考虑的是 minθ E(x,y)∼P L(fθ(x),y)min_{\theta}\ E_{(x, y) \sim P}\ L(f_{\theta}(x), y)
  • 此时, 我们进行采样的分布 PP是确定的, 而要求期望的目标 L(fθ(x),y)L(f_{\theta}(x), y)是不确定的, 随参数不同而变化的
  • 此时对于打分函数, 其中的 fθf_{\theta}往往是黑盒的, 不可导出的(如深度神经网络)
    对于RL,
  • 我们考虑的是 maxθ E(s,a)∼ρπθ,Env r(s,a)max_{\theta}\ E_{(s, a) \sim \rho ^{\pi_{\theta}, Env}}\ r(s, a)
  • 此时, 我们进行采样的分布 ρπθ,Env\rho ^{\pi_{\theta}, Env}是不确定的, 随参数不同而变化的, 而要求期望的目标 r(s,a)r(s, a)是确定性的
  • 此时对于样本服从的分布 ρπθ,Env\rho ^{\pi_{\theta}, Env}, 其中的 ρ\rho 和 πθ\pi_{\theta} 往往都是黑盒的. 两层黑盒进行交互, 叠加在一起, 带来了比传统ML更大的挑战

  • 对于给定的MDP, 不同的策略会采样出不同的(s,a)(s, a)序列对, 策略与序列对在随机变量的意义下一一对应.
  • 对于某个策略及其采样出的序列对, 我们定义占用度量（Occupancy Measure）对它们进行描述

ρπ(s,a)=E[∑t=0TγtI(St=s,At=a)∣π],∀s∈S,a∈A\rho ^{\pi}(s, a) = E[\sum_{t = 0}^{T} \gamma ^t I(S_t = s, A_t = a)|\pi], \forall s \in S, a \in A

=∑t=0TγtP(St=s,At=a∣s0,π)= \sum_{t = 0}^{T} \gamma ^t P(S_t = s, A_t = a|s_0, \pi)

  • 第一行告诉我们, ρ\rho接收一个给定的状态-动作对s,as,a, 返回一个随机变量的期望值
  • 第二行中, 理论上我们应当连带着随机变量S0S_0一起考虑. 但是由于S0S_0的分布与策略无关, 仅由环境决定, 因此我们可以将其作为固定的给定量s0s_0看待.
  • 此处定义的等比衰减求和的形式, 是为了后面定义值函数时, 与MRP的奖励的衰减求和相吻合

状态占用度量

ρπ(s)=∑t=0TγtP(St=s∣s0,π)=∑a′∈Aρπ(s,a′)\rho ^{\pi}(s) = \sum_{t = 0}^{T} \gamma ^t P(S_t = s|s_0, \pi) = \sum_{a' \in A} \rho ^{\pi}(s, a')

给出如下两个定理:

TH1:
和同一个动态环境交互的两个策略 π1\pi_1和 π2\pi_2得到的占用度量 ρπ1\rho^{\pi_1}和 ρπ1\rho^{\pi_1}满足

ρπ1=ρπ2 iff π1=π2\rho^{\pi_1} = \rho^{\pi_2}\ \text{iff} \ \pi_1 = \pi_2

TH2:
给定占用度量ρ\rho, 可生成该占用度量的唯一策略是:

πρ=ρ(s,a)∑a′∈Aρ(s,a′)=ρ(s,a)ρ(s)\pi _{\rho} = \frac{\rho (s, a)}{\sum_{a' \in A}\rho(s, a')} = \frac{\rho (s, a)}{\rho(s)}

证明:
TH1根据TH2不难得到;
对于TH2, 考虑如下事实

ρ(s,a)=ρ(s)π(a∣s)\rho (s, a) = \rho(s) \pi(a|s)

那么, 对于某个给定的占用度量, ρ(s,a),ρ(s)\rho (s, a), \rho(s) 都被确定, 策略当然也是唯一确定的.

更加严谨的证明: U. Syed, M. Bowling, and R. E. Schapire. Apprenticeship learning using linear programming. ICML 2008.

上面两个定理告诉我们:

  • 策略与占用度量是完全的一一对应关系, 是描述同一个东西的两种语言, 互相之间完全等价

定义策略的累积奖励为

V(π)=E[∑t=0∞γtr(St,At)∣s0,π]=∑s,aρπ(s,a)r(s,a)=Eπ[r(s,a)]V(\pi) = E[\sum_{t = 0} ^{\infty}\gamma ^t r(S_t, A_t)|s_0, \pi] = \sum_{s, a} \rho^{\pi}(s, a) r(s, a) = E_{\pi}[r(s, a)]

  • 其中, 第二个等号将期望吸收进了占用度量当中; 第三个等号是RL中的一个简写形式.
  • 强化学习的目标就是最大化上面的累计奖励, 给出使得累计奖励最优的那个π\pi
  • 由于策略与占用度量的关系是黑盒的, 改变策略后, 无法很快得到新的占用度量
  • 因此, 上面的等式没有给出具体的策略优化方法.

策略评估与策略提升

  1. 首先, 我们会推广前面的描述方法, 给出状态价值函数和动作价值函数的定义.
  2. 在定义了上面这些更强的描述手段后, 我们可以进一步定义"策略提升"的概念. 此时, 我们考虑的是"只利用"的确定性策略 π(s)=a\pi(s) = a
  3. 在这之后, 我们证明策略提升定理, 这个定理告诉我们, 贪婪地对策略进行更新是能够导出全局最优的结果的.
  4. 于是, 我们通过贪婪更新的方法, 给出一个策略提升的实际操作过程.
  5. 然后, 我们证明, 对于非确定性的, 综合探索与利用的ϵ\epsilon-greedy策略π(⋅∣s)\pi(\cdot |s), 并证明此时定理依然成立 (对于策略的更新过程中, 改变动作分布这一步骤, 可以探讨其他更改方式)

策略值函数估计（Policy Evaluation）

  • 状态价值

Vπ(s)=E[∑t=0∞γtr(St,At)∣S0=s,π]=Ea∼π(s)[r(s,a)+γ∑s′∈SPsπ(s)(s′)Vπ(s)]V^{\pi}(s) = E[\sum_{t = 0} ^{\infty}\gamma ^t r(S_t, A_t)|S_0 = s, \pi] = E_{a \sim \pi(s)}[r(s, a) + \gamma \sum_{s' \in S} P_{s\pi(s)}(s')V^{\pi}(s) ]

  • 动作价值

Qπ(s,a)=E[∑t=0∞γtr(St,At)∣S0=s,A0=a,π]=r(s,a)+γ∑s′∈SPsπ(s)(s′)Vπ(s′)Q^{\pi}(s, a) = E[\sum_{t = 0} ^{\infty}\gamma ^t r(S_t, A_t)|S_0 = s, A_0 = a, \pi] = r(s, a) + \gamma \sum_{s' \in S} P_{s\pi(s)}(s')V^{\pi}(s')

显然, "状态价值函数"是"策略累计奖励"的推广形式, 而动作价值函数可以看做状态价值函数的自然延伸.

对于两个策略 π,π′\pi, \pi', 定义策略提升:

Qπ(s,π′(s))≥Vπ(s),∀s∈SQ^{\pi} (s, \pi'(s)) \geq V^{\pi}(s), \forall s \in S

注意: 上述不等式中, 采用的价值函数始终是原始策略 π\pi的价值函数. 因此, 某种程度上这是一种局部的最优性质.

我们关心的是, 这种局部最优性能否导出全局上的最优

Qπ′(s,π′(s))=Vπ′(s)≥Vπ(s),∀s∈SQ^{\pi'} (s, \pi'(s)) = V^{\pi'}(s) \geq V^{\pi}(s), \forall s \in S

下面, 我们给出策略提升定理, 它告诉我们, 这种局部到全局的最优性转换是成立的.

策略提升定理（Policy Improvement Theorem）

  • 定理的证明过程反复应用了值函数定义和马尔科夫性质. (有些类似在优化问题中, 凸函数的性质: 局部最优解就是全局最优解. )
  • 马尔科夫性质:

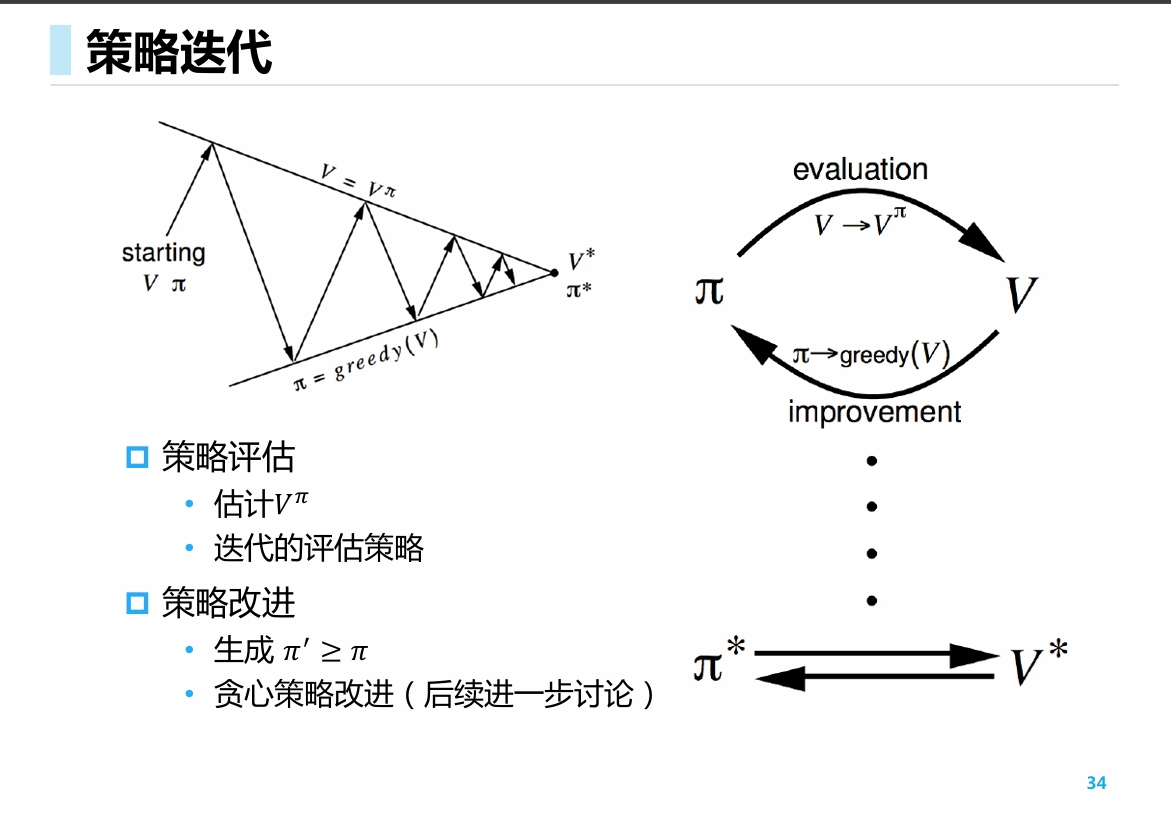
E[Qπ(S,A)]=E[r(S,A)+γVπ(π(A))]E[Q^{\pi}(S, A)] = E[r(S, A) + \gamma V^{\pi}(\pi(A))]

于是, 我们就得到一个进行策略提升的范式:

  1. 给出策略 (这一步是简单的)
  2. 评估策略价值 (这一步是困难的)
  3. 根据当前策略价值寻找局部最优解, 获取新策略 (这一步是简单的)

反复进行, 直至收敛.

策略提升定理 - 在ϵ\epsilon-greedy场景下

  • 前面的讨论中, 我们考虑的策略是确定性的, 对于给定的状态, 它会确定性地返回某个动作.
  • 对于确定性策略进行更新时, 我们简单地将其返回值更改为当前最优解;
  • 倘若我们采用一个 ϵ\epsilon-greedy的策略, 它有 ϵ\epsilon的概率随机返回动作, 那么情况会不会有变化呢?

答案是, 在这种新的策略下, 策略提升定理和"评估 - 提升"的范式依然是成立的.

  • 证明中, 不等式的那一行, 本质上做了一个加权平均. 显然加权平均得到的结果不会超过最大值.
  • 延伸: 对于任意的策略, 我们有可能采用更多样的方式去改变策略的动作选择分布, 而不仅仅是移动ϵ\epsilon-greedy分布中的greedy项.

基于动态规划的强化学习

前面几节中, 我们完成了理论上的一些分析, 并得到了一个提升范式; 现在, 我们介绍运用一个运用动态规划方法的具体实现.

  • 状态价值

Vπ(s)=Ea∼π(s)[r(s,a)+γ∑s′∈SPsπ(s)(s′)Vπ(s)]=Ea∼π(s)[Qπ(s,a)]V^{\pi}(s) = E_{a \sim \pi(s)}[r(s, a) + \gamma \sum_{s' \in S} P_{s\pi(s)}(s')V^{\pi}(s) ] = E_{a \sim \pi(s)} [Q^{\pi(s, a)}]

  • 动作价值

Qπ(s,a)=E[∑t=0∞γtr(St,At)∣S0=s,A0=a,π]=r(s,a)+γ∑s′∈SPsπ(s)(s′)Vπ(s)=r(s,a)+γ∑s′∈SPsπ(s)(s′)∑a′∈Aπ(a′∣s′)[Qπ(s′,a′)]Q^{\pi}(s, a) = E[\sum_{t = 0} ^{\infty}\gamma ^t r(S_t, A_t)|S_0 = s, A_0 = a, \pi] = r(s, a) + \gamma \sum_{s' \in S} P_{s\pi(s)}(s')V^{\pi}(s) = r(s, a) + \gamma \sum_{s' \in S} P_{s\pi(s)}(s') \sum_{a' \in A} \pi(a'|s') [Q^{\pi(s', a')}]

关于策略和值函数, 我们有以下事实

  • 价值函数和策略在优化问题上一一对应. 最优策略的值函数一定是最优的; 给定最优的价值函数, 可以采用 arg⁡max⁡\arg\max的方式导出最优策略
  • 寻找优化策略的方法有两种：策略迭代和价值迭代

此处, 我们先不加证明地给出如下两种方法, 它们都应用了动态规划的方式, 通过策略迭代和价值迭代对最优策略进行求解.

其中

  • 迭代可能是同步的: 存储两份价值函数; 也可能是异步的: 只存储一份价值函数.
  • 策略迭代在直观上更加自然; 值函数迭代可以看做是只进行一步评估的策略迭代
  • 两种方法的收敛性都经过了证明

我们需要证明: 在任意给定的初始策略下, 不断地进行如上操作, 最终结果一定收敛, 程序一定会终止, 且结果一定是最优解.

其中, 收敛性的证明分为两个方面:

  1. 求解价值函数时, 求解的过程是收敛的
  2. 不断更新策略时, 更新的过程是收敛的
    具体而言, 对于这两个算法, 我们分别考虑了两个算子, 并证明了它们是压缩映射. 然后, 我们通过不动点定理, 证明了不断应用这个压缩映射一定会导出一个柯西点列, 并就此证明了其收敛性质.

论证的大致思路如下:

We are going to prove this using the Banach fixed point theorem by showing that the Bellman optimality operator is a contraction over a complete metric space of real numbers with metric L-infinity norm. For this, we will first discuss the fixed point problem and complete metric spaces with respect to the Cauchy sequence.

具体的细节证明在 2024-10-16中给出. 参考资料为
Mathematical Analysis of Reinforcement Learning — Bellman Optimality Equation | by Vaibhav Kumar | Towards Data Science

此处, 对于两种动态规划算法, 在理论证明方面几乎花费了一整天的功夫;
但是倘若不考虑理论证明, 只是从思想上和直观感受上进行理解, 并从code上进行具体实现, 那么本节的内容还是十分自然的

基于模型的强化学习

  • 前面我们的所有分析, 都是基于MDP属于白盒环境的前提下进行讨论的
  • 在MDP未知的时候, 理论上可以通过episode进行模拟, 将MDP环境建模出来, 然后进行学习.

简单来说, 就是采用"用样本均值代替期望"的方法,

Pss′a=N(s,a)N(s,a,s′)P_{ss'}^{a} = \frac{N(s, a)}{N(s, a, s')}

Rsa=∑(r(i)(s,a))N(s,a)R_{s}^{a} = \frac{\sum(r^(i)(s, a))}{N(s, a)}

总结

What’s more

以上的全部讨论都是基于MDP给定的前提. 而在下面, 我们会考虑MDP未知的情况, 讨论不对MDP建模, 直接依靠episode进行学习的方法, 如

  • MC 蒙特卡洛方法
  • 时序差分

几种方法的思想与树搜索中的BFS, DFS隐隐之间竟有呼应, 十分有趣.

backtop