Note

基于上海交通大学强化学习课程系列课程学习RL的笔记.
SJTU RL Course (wnzhang.net)

此为第二讲内容的杂项. 由于两个动态规划算法: 策略迭代算法和价值迭代算法的严格证明内容比较多, 于是将其单独列为一篇Blog记叙于此.

主要参考的资料为
Mathematical Analysis of Reinforcement Learning — Bellman Optimality Equation | by Vaibhav Kumar | Towards Data Science

包含此定理在内的其他相关数学证明可以在
rl-proofs.pdf (wnzhang.net)
中找到.

此处, 我们用收缩算子和不动点定理, 证明用期望算子不断进行操作最终会得到收敛的解;
而在实际的通过样本进行操作的算法中, 这个证明就不适用了. 相关的证明需要通过随机逼近的方法完成, 详见pdf, 此处不作赘述.

存在性证明:

对于给定的MDP:

<S,A,Pss′a,Rsa,γ><S, A, P_{ss'}^{a}, R_s^{a}, \gamma>

假定 S,AS, A均为有穷集合, Pss′a,RsaP_{ss'}^{a}, R_s^{a} 为条件随机变量.

考虑函数 V:π,s→RV: \pi, s \rightarrow R. 在 π\pi给定的情况下, VV等价于向量

[V(s1),V(s2),...,V(s∣S∣)]∈R∣S∣[V(s_1), V(s_2), ..., V(s_{|S|})] \in R^{|S|}

所以, {π}\{\pi\}与 R∣S∣R^{|S|}的某个子集可以构建一一映射.

对于给定了两个迭代过程, 等价于给定了随机的初始向量 V0V_0, 并给定了Bellman算子 BB. 现在, 要求证明:

  • 重复应用Bellman算子, ViV_i将会收敛于最优解 V∗V^*. 且 V∗V^*会出现在向量序列当中.
  • 其中, 两个问题中包含的Bellman算子各不相同. 分别为

BV(s)=∑a∈Sπ(a∣s)[Rsa+γ∑s′∈SPss′aV(s′)]BV(s) = \sum_{a \in S} \pi(a|s) [R_{s}^{a} + \gamma \sum_{s' \in S} P_{ss'}^{a} V(s')]

BV(s)=max⁡a∈A[Rsa+γ∑s′∈SPss′aV(s)]BV(s) = \max_{a \in A} [R_{s}^{a} + \gamma \sum_{s' \in S} P_{ss'}^{a} V(s)]

对于两个算子, 我们都通过以下两个步骤, 证明反复应用算子能够使得 VV收敛:

  1. 根据相关定义, 证明两个算子都是压缩映射.
  2. 根据Banach fixed point theorem, 得到反复应用压缩映射会得到一个柯西点列, 并顺势得到序列的收敛性.

其中:

  • 大量的基础定义以图片形式给出
  • Banach fixed point theorem 的证明以图片形式给出

压缩映射性质的证明如下:

不动点定理与其余相关定义的证明如下:

Metric space

Cauchy sequence

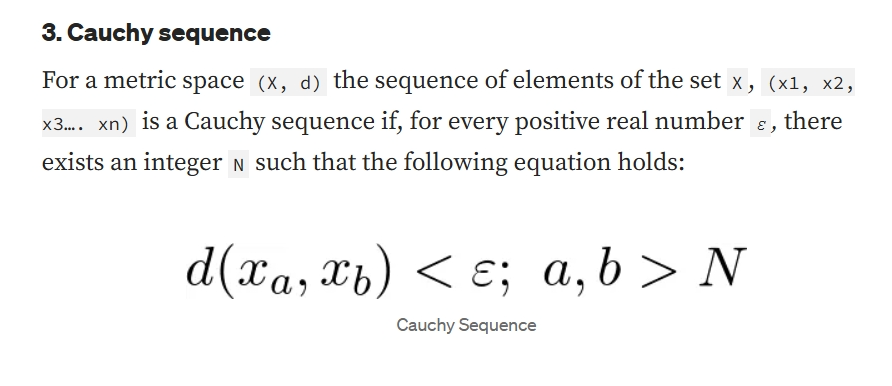
Complete Metric space

Contraction

Banach fixed point theorem

分为两部分证明

  • 按照常理来说, 证明了柯西点列的性质应该就够了, 因为柯西点列保证了极限的存在性和唯一性
  • 但是谨慎起见, 这里还是贴出唯一性的证明

唯一性的证明:

存在性的证明:

  1. 反复应用三角不等式, 将其拆分为多项和的形式

  2. 反复应用压缩映射的性质, 提出一系列等比衰减的权重, 并通过前n项和将其吸收为一个系数.

  3. 由于nn能够足够大, 于是系数能够足够小, 满足小于ϵ\epsilon的条件. 就此, 我们得到反复应用压缩映射的结果序列是柯西点列, 并得到了它的收敛性.

以下, 为对于第二个算子的证明(即对于价值迭代方法的收敛性证明)

Coming back to the Bellman Optimality Equation

回到具体的RL问题, 我们定义
The Bellman Operator:

BV(s)=max⁡a[Ras+γ∑s′∈SPss′aV(s′)]BV(s) = \max_{a} [R_{a}^{s} + \gamma \sum_{s' \in S} P_{ss'}^{a}V(s')]

采用无穷范数的Metric space (X,d), 其中X的元素为由值函数生成的向量

V=[V(s1),V(s2),...,V(s∣S∣)]∈R∣S∣V = [V(s_1), V(s_2), ..., V(s_{|S|})] \in R^{|S|}

d为向量的无穷范数

∥X∥∞=max⁡i=1,...,∣S∣∣Xi∣\|X\|_{\infty} = \max_{i = 1, ..., |S|} |X_i|

Theorem: Bellman operator B is a contraction mapping in the finite space (R, L-infinity)

Hence, by the Banach fixed point theorem, we conclude that there exists a unique optimal value function V* for every MDP. Using this V*, we can derive the optimal policy π*.

Hence proved, for any finite MDP, there exists an optimal policy π* such that it is better than or equal to every other possible policy π.

Powered By Valine
v1.5.1
backtop