基于上海交通大学强化学习课程系列课程学习RL的笔记.
SJTU RL Course (wnzhang.net)
此为第三讲的内容. 在第二讲中, 我们解释了MDP的概念, 并在MDP处于白盒环境的前提下, 给出了通过期望算子不断进行迭代, 最终得到最优策略的算法. 而在这一讲中, 我们考虑根据一批样本来估计出一个值函数的方法, 包括MC方法和TD方法.
TODO: 编写值函数估计相关的库函数, 包括DP, MC, TD三种实现的函数
预计在gym环境上对这些函数进行测试
相关gym环境强化学习基础篇(十)OpenAI Gym环境汇总 - 简书 (jianshu.com)
无模型的强化学习(Model-free RL)
- 前面一讲中, 我们考虑的都是显式给出各种分布(如状态转移分布和奖励函数等)的MDP白盒环境
- 而在实际场景中, 我们往往无法得到相关的分布, 只能得到从分布中采样得出的一系列样本episode.
- 模型无关的强化学习直接从经验中学习值(value)和策略 (policy),而无需构建马尔可夫决策过程模型(MDP)
值函数估计
在白盒环境中, 我们根据如下公式来对值函数进行计算
V(s)=E[Gt∣St=s]=E[i=t∑Tλi−tRi∣St=s]=E[RStAt+λV(St+1)∣St=s]
其中, 将期望展开可以得到
V(s)=a∈A∑aπsa[Rsa+λs′∈S∑Pss′aV(s′)]
而在黑盒情况下, 我们无法直接对相关的期望进行求解, 只能通过"样本均值"对期望进行拟合.
于是,
- 将原本要求解的期望目标 Ri化为样本均值 ∑iNri/N, 我们得到了蒙特卡洛的方法
- 将原本要求解的期望目标 V(t)(St+1)化为样本相关的 V(t−1)(St+1), 我们得到了TD的方法
结合前面的直接求解法以及DP求解法, 可总结归纳如下:
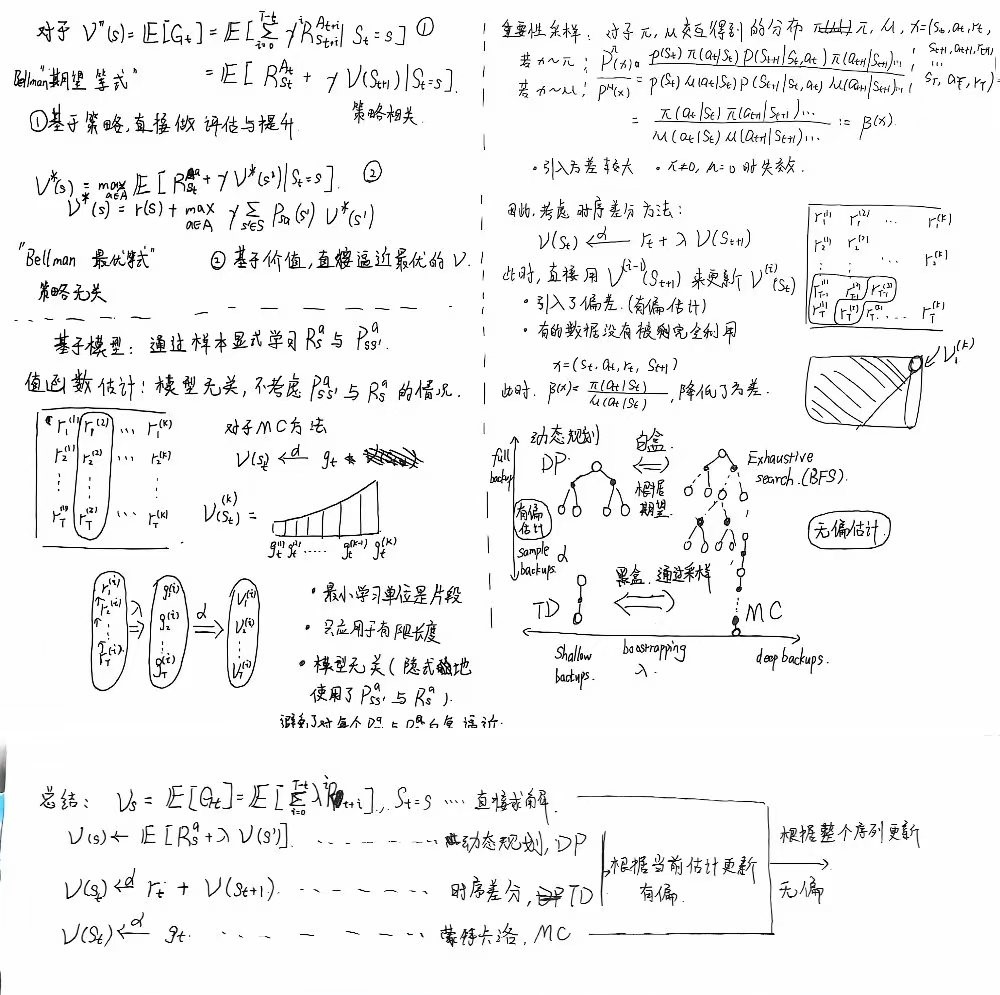
蒙特卡洛值估计 MC

- 大致思想上与前面讲的一致, 即用样本均值 ∑iNri/N 来近似 Ri.
- 有一点不同的是, 此处不是对所有的 Ri做简单平均, 而是做了加权平均和来获取最终的期望目标 E[Gt]. 具体的加权分布与参数 α 有关
- 关于 λ与 α:
- λ越大, agent在每个episode中越关注未来奖励, 假定环境需要长远地考虑
- α越大, agent在训练时越关注近期的episode, 而忽略历史的episode, 假定环境的变化性是比较强的
重要性采样 (离线蒙特卡洛)
此处我们考虑重要性采样, 从而引出TD方法.
假设我们有从分布q中采样得出的一系列样本x, 并想要通过这些样本来求出p的期望, 那么可做如下变化
Ex∼p[f(x)]=∫xp(x)f(x)=∫xq(x)q(x)p(x)f(x)=Ex∼q[q(x)p(x)f(x)]
于是, 我们就可以将q中采样得到的x加上一个重要性权重 β(x)=q(x)p(x), 然后求出它们的期望(通过样本均值), 就可以得到想要的p的期望.
在RL中, 我们采用MC方法时采样得到的样本为 x=[st,at,rt,...,sT,aT,rT]
根据策略 π与 μ和环境交互导出的分布, 我们可以导出重要性权重:
β(x)=p(st)μ(at∣st)P(st+1∣st,at)...p(st)π(at∣st)P(st+1∣st,at)...=μ(at∣st)μ(aa+1∣st+1)...π(at∣st)π(at+1∣st+1)...
于是, 我们通过这种方法可以做到:
- 根据某个行为策略采集到的数据不断更新目标策略
- 目标策略不需要在线地与环境进行交互
根据权重函数, 容易得到
- 我们无法在𝜋非零而𝜇为零时使用重要性采样
- 重要性采样将显著增大方差(variance) (许多概率进行了连乘, 方差也随之增大)
由于上面的缺点, 我们引入了TD.
时序差分学习(Temporal Difference Learning

- 引入了随机变量的等式 V(s)=E[RStAt+λV(St+1)∣St=s]
- 通过迭代式 V(st)→αrt+V(st+1) 来逼近期望等式.
因此, TD方法可以在episode还未结束时就更新策略, 并实时地采用新策略不断进行采样, 实现在线的控制.


多步时序差分学习
定义n步回报
gt(n)=rt+λrt+1+...+λn−1rt+n−1+λnV(st+n)
更新公式为
V(s)←αgt(n)
- 一方面, 利用了许多当前获取的回报r, 另一方面, 还是使用了历史数据V(s)对后续的大量r进行估计
- 介于MC与一步TD之间.
总览强化学习值函数估计多种方法

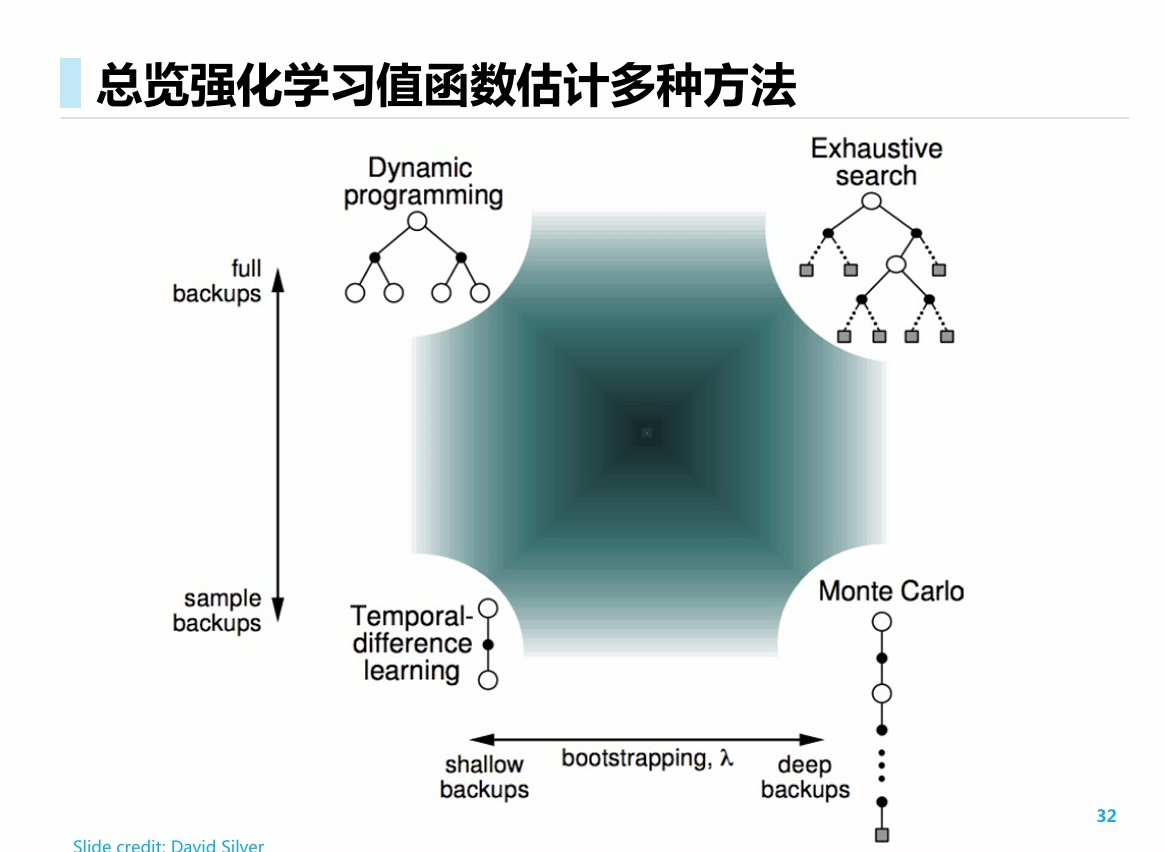







![[RL] 第三讲: 值函数估计](/images/24-10/24-10-16-01.png)
