[RL] 第四讲: 无模型控制方法

基于上海交通大学强化学习课程系列课程学习RL的笔记.
SJTU RL Course (wnzhang.net)

• 在第三讲中, 我们讲述了采样方法下, 对值函数进行估计的办法; 估计完毕值函数之后, 会作策略提升;
• 这一讲中, 我们讲直接作价值提升的算法.
• 可以理解为贪婪的值函数更新方法, 直接在每一步都对策略进行更新.
• SARSA, Q-learing, 多步自助方法.

各种方法的三重维度:

• 取期望 vs 大数定理采样 (BFS vs DFS)
• 多步迭代拟合后提升 vs 一步后直接max作提升 (策略迭代 vs 价值迭代)
• 对T步数据进行学习(无偏) vs 对一步数据进行学习(有偏) (MC vs TD)

考虑价值函数拟合完毕后, 做策略提升的方式:

选出最优动作, 进行相关更新(greedy, $\epsilon$-greedy, 或考虑softmax)

$$\pi(s) = {\arg \max}_{a} V(s) = {\arg \max}_{a} E[R + V(S')]$$

此处引入了两个随机变量 $R, S'$, 要求解它们都是环境相关的;

而对于Q价值函数, 我们考虑最优动作:

$$\pi(s) = {\arg \max}_{a} Q(s, a)$$

此时得到的值是价值无关的. 因此, 站在某个状态要对动作进行评估时, 采用Q函数指导可以在不涉及环境的情况下之间得到动作打分.

所以, 在进行策略迭代算法的时候, 我们考虑的都是Q函数.

SARSA

类似TD, 对于每个五元组样本

$$<s_t, a_t, r_t, s_{t+1}, a_{t+1}>$$

做策略评估:

$$Q(s, a) \leftarrow^{\alpha} r + \gamma Q(s', a')$$

• 每一步更新$Q$函数之后, 都直接根据$Q$函数的指导进行下一个动作的选取
• 相当于每读入一个五元组样本, 都对值函数以及策略做了一次更新.
• 而之前的TD与MC, 都是至少读入了一定的episode之后, 再对策略进行更新.

on-policy TD control

• 在线策略时序差分控制（on-policy TD control）使用当前策略进行动作采样。
• 即，SARSA算法中的两个“A”都是由当前策略选择的
• 因此, 可以应用在某些不终止的环境当中; 不需要片段终结就能进行学习, 并且完成策略的更新

Q-学习

离线(off-policy)的学习方法.

什么是离线策略学习

• 目标策略𝜋(𝑎|𝑠)进行值函数评估（𝑉 (𝑠)或𝑄 (𝑠,𝑎)）
• 行为策略𝜇(𝑎|𝑠)收集数据： $\{s_1, a_1, r_1, s_2, a_2, r_2, ..., s_T, a_T, r_T\}$ ~𝜇

为什么使用离线策略学习

• 平衡探索（exploration）和利用（exploitation）
• 通过观察人类或其他智能体学习策略
• 重用旧策略所产生的经验
• 遵循探索策略时学习最优策略
• 遵循一个策略时学习多个策略

做法:

• 采集样本时, 始终使用行为策略(如, $\epsilon-$greedy)
• 进行训练时, 先将采集到的样本补全, 然后训练目标策略(如, greedy)
• 训练和拟合的值函数是同一个, 它们导出了两种策略

给定 $s, a, r, s'$, 作

$$Q(s, a) \leftarrow^{\alpha} r + \max_{a'} \gamma Q(s', a')$$

此时, 虽然我们用一个策略的样本去训练另一个策略, 但是无需进行重要性采样

• 此时, 给定的是 $s, a, r, s'$, 训练时的$a'$是通过目标策略产生的, 所以训练样本服从策略的分布
• 实际执行的动作通过行为策略产生, 此时实际动作不符合目标策略的分布, 但是没有用于训练所以没关系.

收敛性证明:

• 期望意义上的收敛用收缩算子证明
• 实际操作过程中的收敛性用随机逼近（stochastic approximation）方法进行证明. 用到了引理5.1"满足特定性质的随机逼近过程收敛". Tsitsiklis J N. Asynchronous stochastic approximation and Q-learning。

两种证明有些类似. 我们都是给出RL中的操作, 如期望迭代或随机逼近过程, 再证明其满足某些性质, 如作为一个收缩算子或作为特定类型的随机逼近过程, 最后证明这样的性质可以导出收敛性, 如根据不动点定理和引理5.1

详细的证明见
rl-proofs.pdf (wnzhang.net)

TODO: 了解随机过程的证明方法和思路. 涉及到没听过的领域, 可能没有办法详细领悟透彻, 只能理解大致思路

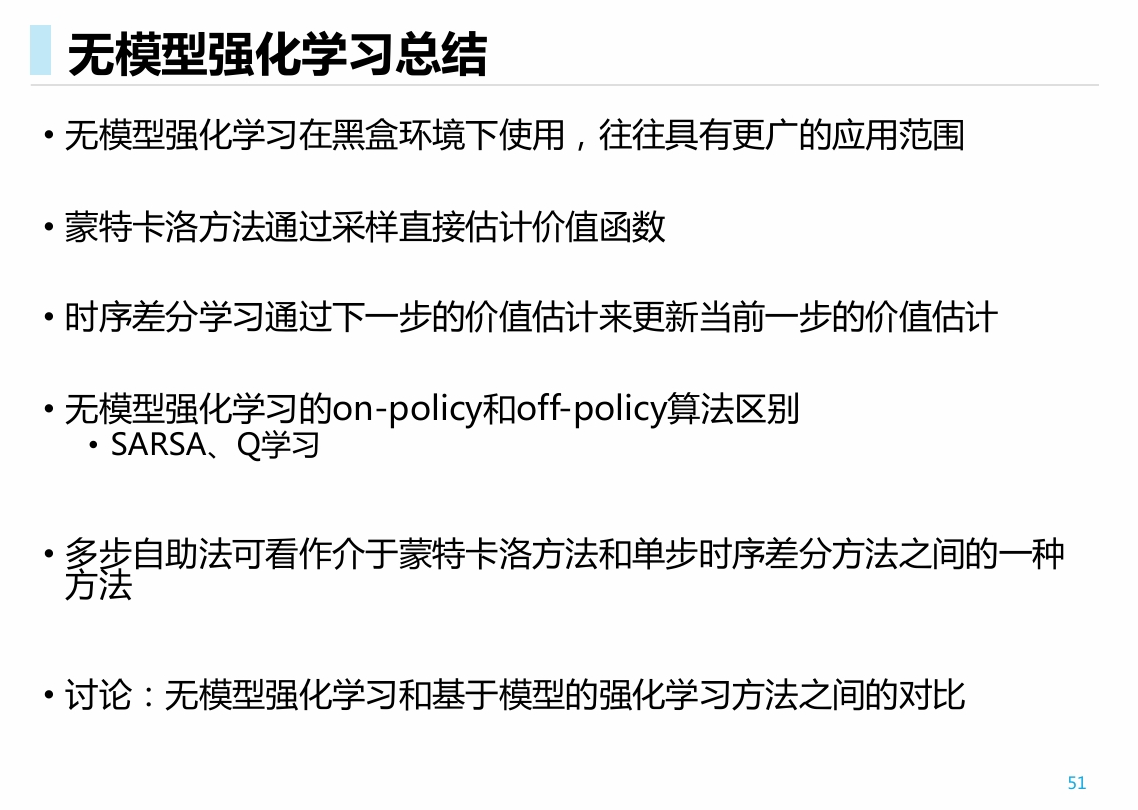
比较: 通过迭代公式进行比较. 有三个维度可以考虑这些公式:

• 期望公式(白盒, DP实现) vs 迭代公式(黑盒, 实际算法, 如MC, TD, SARSA, Q)
• 转移等式(策略迭代中值函数估计, MC, TD) vs 最优等式 (价值迭代, SARSA, Q)
• 依据V函数 vs 依据Q函数

多步自助法

1. 多步时序差分预测
2. 多步Sarsa
3. 使用重要性采样的多步离线学习法
4. 多步备份树算法

多步时序差分

考虑到, MC相当于是$T$步的时序差分, 我们可以提出n步时序差分的概念:

对样本 $<s_0, a_0, r_0, ..., s_{n-1}, a_{n-1}, r_{n-1}>$,
做更新

$$V(s_0) \leftarrow _{\alpha} g_0^{(n)} + \lambda^n V(s_n)$$

相当于: 一部分信息从n对三元组中得到, 一部分信息从已有的先验分布得到

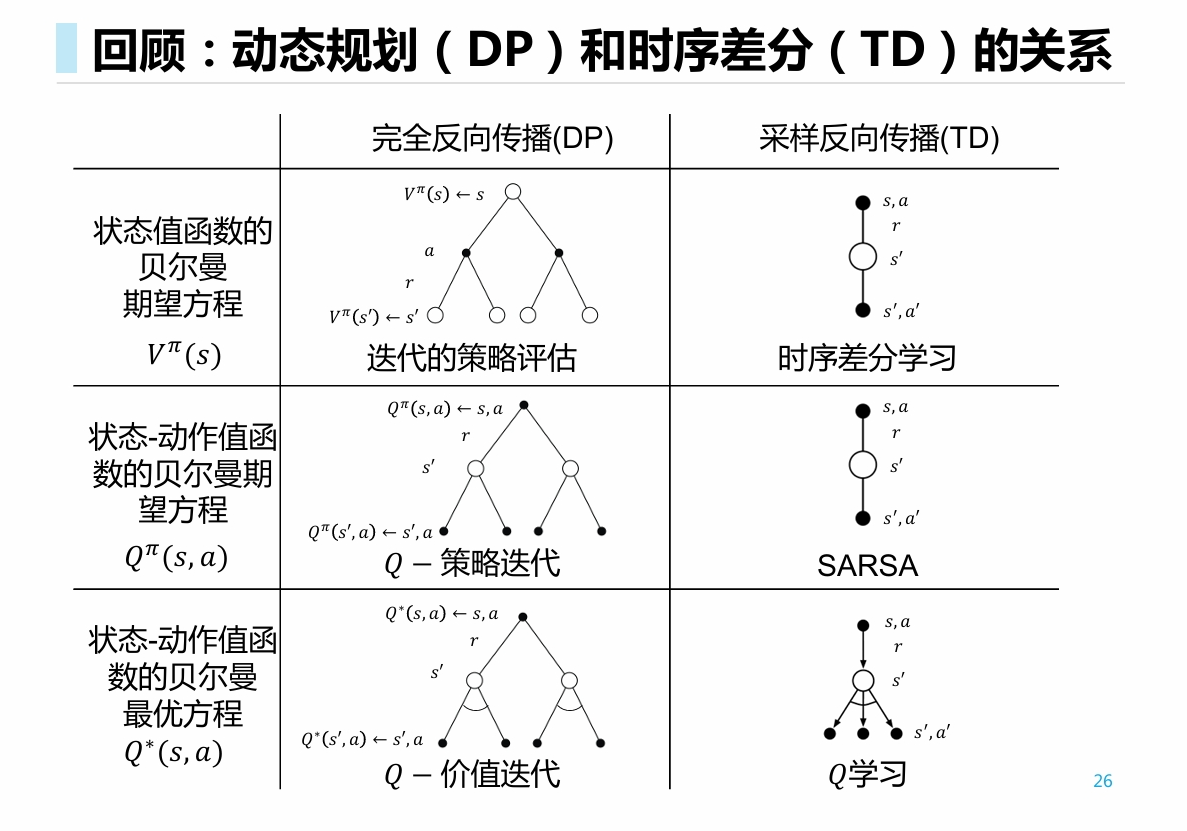
使用平均𝑛步累计奖励的𝐓𝐃 𝝀 算法

$$V(s_t) \leftarrow _{\alpha} g_t^{\lambda}$$

将所有 $i$步方法结合在一起:

• $\lambda =1$时, 相当于MC方法
• $\lambda =1$时, 相当于单步TD方法
• 类似不断地套娃综合, 将多种方法结合在一起.
• 某种程度上可以看做是权重形式更加复杂的广义MC方法.

多步SARSA

• 前面多步的思想都是在MC和TD等值函数评估方法上考虑
• 通过将n步的思想应用在价值迭代上, 得到多步SARSA以及多步Q

$$Q(s, a)\leftarrow_{\alpha} g_t^{n} + Q(s_{t+n}, a_{t+n})$$

考虑某条仅有一个状态的奖励非0的episode

• 对于原始的SARSA, 仅更新了与之相关的一个状态的动作取值
• 对于n步SARSA, 更新了n个状态取值

假设考虑一个长度为T的episode, 各个算法的具体的执行过程如下

• 原始MC: 对于长度T的样本, 更新1次
• 单步TD / SARSA: 对于长度1的样本, 更新T次
• n步TD / SARSA: 对于长度为n的样本, 更新T-n次

可见, 某种程度上, n的取值应当不大不小, 此时更新量的总和最大, 同时最好地平衡了偏差和方差

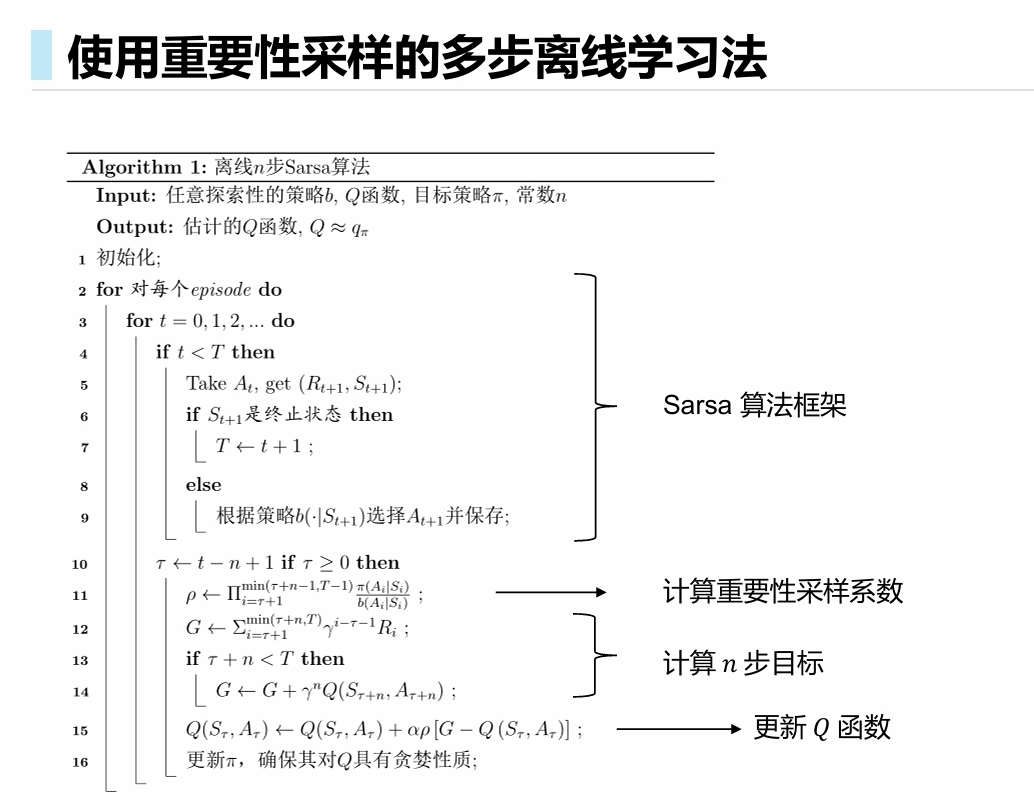
使用重要性采样的多步离线学习法

推导过程类似. 对于n步的离线更新算法, 会添加一个n项分式连乘的重要性修正值, 从而将执行策略分布修正为目标策略分布.

多步树回溯算法(N-step Tree Backup Algorithm)

不需要重要性采样的算法

• 𝑄学习和期望Sarsa(expected Sarsa)

$$g_{t:t+n} = r_t + \lambda \sum_{a\neq a_{t+1}} \pi(a|s_{t+1}) Q(s_{t+1}, a) + \lambda \pi(a_{t+1}| s_{t+1}) g_{t+1:t+n}$$

$$Q(s_t, a_t) \leftarrow_{\alpha} g_{t:t+n}$$

• 既出让了一部分偏差, 又出让了一部分方差
• 统计了n个已知的r, 出让了方差来减小偏差
• 使用了先验的$Q(s_{t+1}, a)$, 出让了偏差来减小方差

对于单步情况

$$Q(s_t, a_t) \leftarrow_{\alpha} g_{t:t+n} = r_t + \lambda \sum_{a} \pi(a|s_{t+1}) Q(s_{t+1}, a)$$

对比单步动态规划:

$$Q(s_t, a_t) \leftarrow_{\alpha} r_t + \lambda \sum_{s_{t+1}} P(s_{t+1}|a, s_{t}) \sum_{a_{t+1}} \pi(a|s_{t+1}) Q(s_{t+1}, a_{t+1})$$

单步TD(公式上与SARSA相同, 不过策略在episode结束后才进行提升):

$$Q(s_t, a_t) \leftarrow_{\alpha} r_t + \lambda Q(s_{t+1}, a_{t+1})$$

某种程度上, 这个算法综合了期望和采样:

• 对于策略相关的概率分布, 显式求取期望. (此时通过求期望得到了a’, 并选择信任已有的先验信息)
• 对于环境相关的概率分布, 如转移函数等, 通过不断采样来隐式逼近 (考虑的每个样本对都是已经采到的 $<s_t, a_t, r_t, s_{t+1}>$)

总结