LearnLog

基于上海交通大学强化学习课程系列课程学习RL的笔记.
SJTU RL Course (wnzhang.net)

前面我们讨论了许多黑盒的方法, 在那些方法中我们并不考虑环境, 而是直接从数据片段进行学习. 而现在, 我们将尝试获取一个模拟环境, 并通过模拟数据来学习.

课程回顾:

基于模型的动态规划

  • 值迭代: V(s)=r(s)+max⁡a∈Aλ∑Pss′aV(s′)V(s) = r(s) + \max_{a \in A} \lambda \sum P_{ss'}^{a} V(s')
  • 策略迭代: π(s)=arg⁡max⁡a∈Aλ∑Pss′aV(s′)\pi(s) = \arg\max_{a \in A} \lambda \sum P_{ss'}^{a} V(s')

无模型的RL:

  • 在线策略蒙特卡洛 V(st)←αgtV(s_t) \leftarrow ^{\alpha} g_t
  • 在线策略时序差分 V(st)←αr+λV(st+1)V(s_t) \leftarrow ^{\alpha} r +\lambda V(s_{t+1})
  • 在线策略时序差分 SARSA (直接指导策略) Q(st,at)←αr+λQ(st+1,at+1)Q(s_t, a_t) \leftarrow ^{\alpha} r + \lambda Q(s_{t+1}, a_{t+1})
  • 离线策略时序差分 Q学习 (允许离线, 同时学习) Q(st,at)←αr+λmax⁡a′Q(st+1,a′)Q(s_t, a_t) \leftarrow ^{\alpha} r + \lambda \max_{a'} Q(s_{t+1}, a')

策略提升定理:
价值评估指导策略提升

如何更精确地评估价值?

规划与学习

模型: 可以分为分布模型及样本模型(白箱状态, 可写出分布的模型及黑箱状态, 只能进行采样的模型.)

规划: 状态空间的规划 / 规划空间的规划(将规划本身作为空间考虑. 此处规划可以是一个动作结合和动作顺序的约束)

本节课主要围绕状态空间的规划.

通用框架:

  • (将真实数据拿来构建模型)
  • 通过模型采样得到模拟数据
  • 通过模拟数据更新值函数, 从而改进策略

Dyna. 引入了模拟经验的Q学习:

对比普通的方式, 能够更快收敛, 同时更好应对变化的环境.

Dyna-Q+

在原始的奖励值中加上了一个鼓励探索的正则项.

r′=r+Kηr' = r + K \sqrt{\eta}

采样方法

  • 均匀采样: 将很多不重要的状态进行了反复访问.
  • 后向聚焦 backward focusing: 很多状态的值变化会带动前续状态的值发生变化.
  • 优先级采样: 给状态设定优先级, 根据优先级采样.

期望更新与采样更新:

  • 期望更新需要分布模型, 计算量大, 没有偏差
  • 采样更新只需要采样模型, 计算量需求低, 有采样误差(smapling error)
  • 轨迹采样: 计算量少, 不需要分布, 简单有效; 缺点: 不断重复已经访问过的状态 (类似MC)

决策时规划

实时DP(RTDP)
相比传统DP: 跳过了大量策略无关的状态. 只更新轨迹访问的状态值

https://towardsdatascience.com/solving-racetrack-in-reinforcement-learning-using-monte-carlo-control-bdee2aa4f04e

https://github.com/thunderInfy/Racetrack

期望意义下的单步TD.

决策时规划 vs 背景规划:
Background Planning 更新很多状态值, 供之后的选择使用.
Decision-time Planning 着眼于当下, 在不需要快速反应的游戏中很有用.

启发式算法

  • 在当前的状态, 对后续可能的情况进行展开.
  • 回溯到当前节点, 更新当前的值函数.
  • 贪婪策略在单步情况下的扩展.
  • 搜索量越大, 越接近最优 (贪婪的扩展, 完全DP的妥协)

Rollout算法

  • 从当前状态进行MC.
  • 选取估计值最高的动作.
  • 不断重复
  • 类似未给定分布时的 启发式算法.

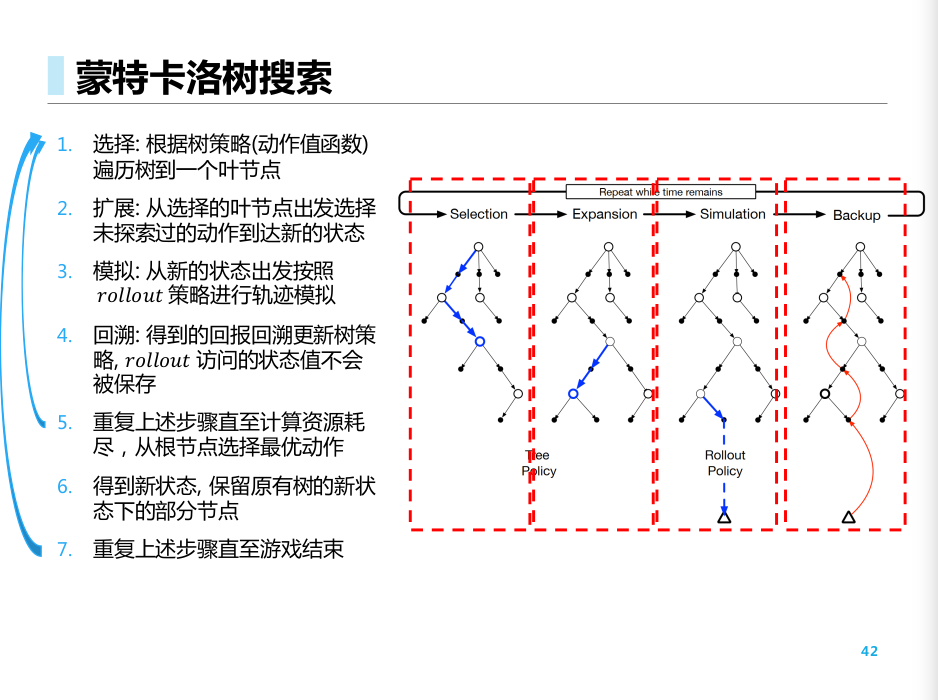
MCTS

  • 选择叶子节点
  • 扩展节点
  • Rollout模拟所在节点, 回溯更新很多节点的值函数. rollout 节点不保存
  • 不断重复, 直到资源耗尽
  • 得到新状态, 保存原来树新状态下的节点.

backtop