[ControlSystem] Ch1, Ch2 系统数学模型

学习控制理论课程PPT的记录. 相关笔记会另开博客记录. 也可能不会开.

主要内容:

1. Ch1 引入控制系统的一些基本概念
2. 引入微分方程的描述方法.
3. Ch2.2 引入线性模型的概念, 线性近似, 线性常微分方程
4. 2.3 引入拉普拉斯变换, 对常微分方程进行求解.

Ch1 控制系统导论

• 什么是控制?
  使受控对象产生预期响应, 按照预期方式工作.

常用微分方程组模型来描述其动态行为和表现

• 什么是自动控制?

无人参与的情况下, 使受控对象产生预期响应
简单对象, 有限目标, 二阶对象为蓝本(妥协)

控制理论简史:

1. 经典控制理论: 20世纪50年代. 以传递函数为基础 研究单输入, 单输出 SISO 线性定常系统
2. 现代控制理论: 20世纪50-60年代. 以状态空间方法为基础, 研究多输入, 多输出 MIMO, 非线性, 时变系统

基本概念

• 控制: 使受控对象按预期方式工作

• 受控对象有多个受控变量

• 控制量 u(t) -> 输出 y(t)

• 自动控制: 无人的情况下, 控制装置根据受控变量自行运行

• 控制系统: 一系列元件组成的系统, 能提供预期的响应.

• 控制系统框图: 表示控制系统的因果关系

• 开环控制: 执行机构直接控制受控对象

• 闭环控制: 受控量作为反馈量进入输入中

• 正反馈 / 负反馈

• 基本性能要求: 稳定性, 快速性, 准确性

Ch2 系统数学模型

• 掌握控制系统的模型建立、线性近似和等效化简方法
• 掌握线性常微分方程的求解方法

物理系统的微分方程模型

• 受控对象可能十分复杂, 所以我们要抓住主要矛盾, 做出妥协
• 通过微分方程, 建立对象的数学模型 (以传递函数 / 状态空间方程为基础)

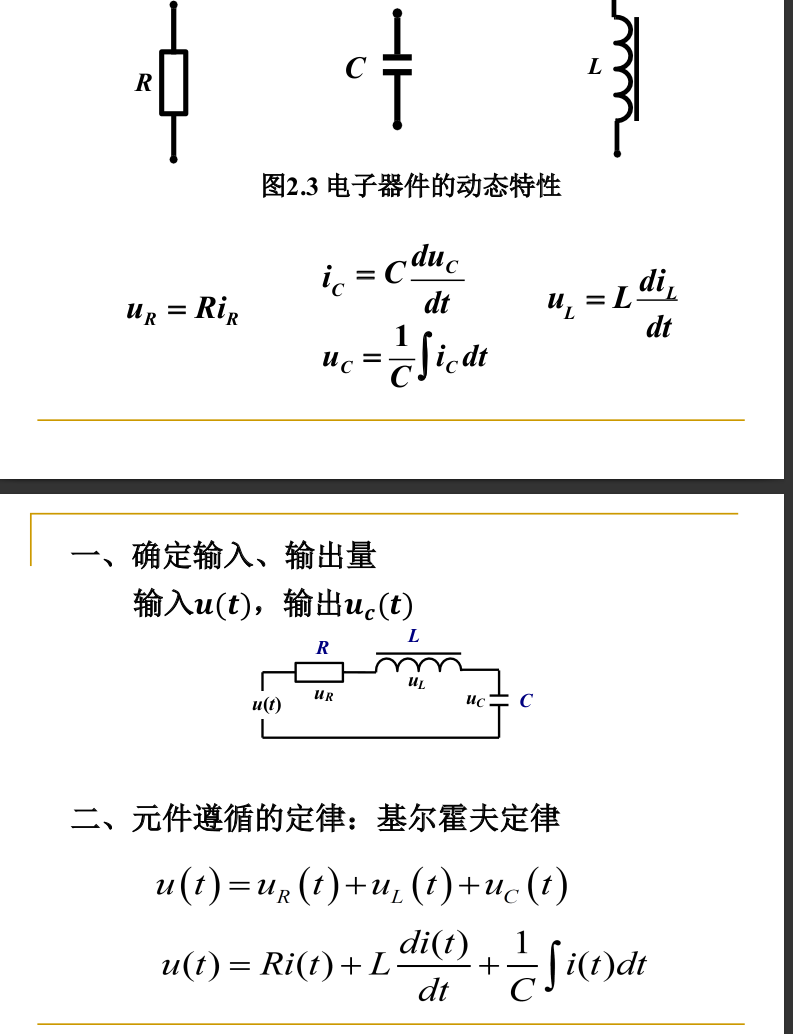
实例: 对于RLC电路的微分方程. (看不懂. 研究弹簧运动的例子就行了吧. )

建立过程:

1. 确定输入量, 输出量
2. 根据元件特性建立动态方程
3. 消去中间量
4. 标准化: 右边为输入变量, 左边为输出变量

两个例子: RLC电路和加速度器

• RLC电路: 电阻, 电容, 电感的性质, 基尔霍夫定律

• 加速度计: 弹簧, 粘性阻尼的性质, 牛顿定律

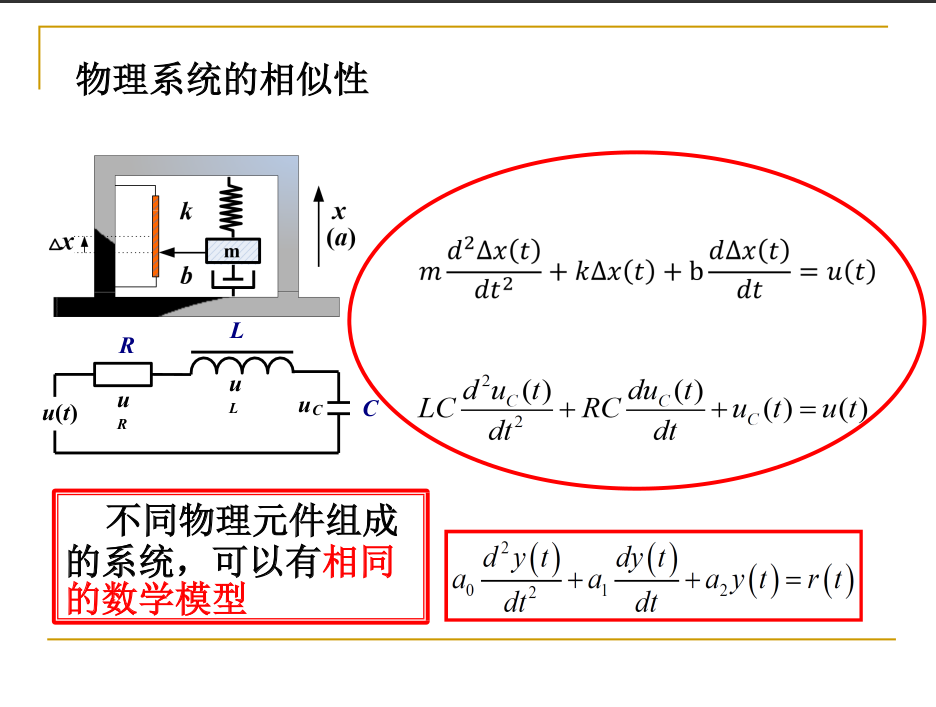
它们的相似性:

非线性系统的例子:

• 单摆系统: $$\ddot{\theta} + \frac{g}{L} \sin \theta = 0$$
• 混沌系统: Lorenz方程 (复杂非线性)

非线性系统数学模型的线性化

• 多数情况下, 线性微分方程足以近似现实世界
• 本课程只讨论 线性定常 (时不变) 模型

线性系统: 满足叠加性和齐次性

n阶线性定常微分方程是线性系统

常见非线性系统: 饱和的放大器, 电机死区, 齿轮间隙

线性近似: 限定范围至线性区, 或考察一个小信号(做泰勒展开后截断)

小结:

1. 线性常微分方程 模型可以很好地描述大量受控变量的动态行为
2. 非本质非线性可以用近似线性常微分方程模型来描述

线性常微分方程的求解

• 普通方式求解, 技巧性很强
• 微分方程具有性质: 引入一个新的积分变量, 对方程的每个项做同样的积分操作, 等式依然成立(由于左右两边同时积分, 以及积分的可加性得到)
• 于是, 我们引入了一种普遍的数学方法: 傅立叶变换

即: 对于原来的和 $f(t)$ 有关的式子, 我们对所有 $f(t)$ 作傅立叶变换, 得到新的式子依然满足微分方程.

$$F(w) = \int_{-\infty}^{+\infty} e^{-jwt} f(t)\ dt$$

$$f(t) = \frac{1}{2 \pi} \int_{-\infty}^{+\infty} F(w)e^{jwt}\ dw$$

傅立叶变换是傅立叶级数的极限形式.

不同频率的谐波信号的组合强度系数

$$a_k = a(k w_0)$$

在频率域决定了时间域信号. (给定一个 $w_0$, 输出一个 $a_k$. 根据这些系数获得时间信号)

称为离散谱函数 (给定一个基频和生成出的一系列频率, 得到对应的一系列系数)

当基频趋近于0时, 就在频率域定义了傅立叶连续谱函数

拉普拉斯变换

• 对于任意的 $f(t)$ 其傅立叶级数可能发散.
• 因而, 我们引入拉普拉斯变换. 将自变量从实数变为复数

$$F(s) = \int_{0}^{\infty} f(t) e^{-st}\ dt$$

拉普拉斯变换是线性变换 (因为是积分变换. )

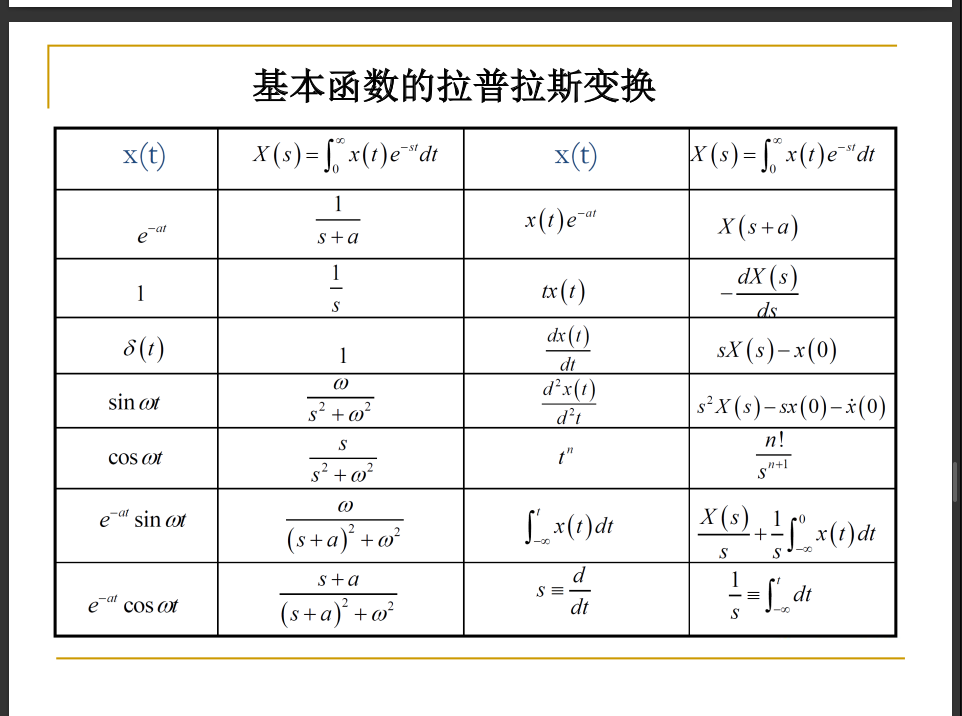
常见拉普拉斯变换:

• $f(t) = A e^{-at} \rightarrow F(t) = \frac{A}{s+a}$
• $f(t) = 1(t) \rightarrow F(t) = \frac{1}{s}$
• $f(t) = At \rightarrow F(t) = \frac{A}{s^2}$
• $f(t) = t^n \rightarrow F(t) = \frac{n!}{s^{n+1}}$

根据欧拉公式 $e^{jwt} = \cos wt + j \sin wt$
有

• $\sin wt = \frac{1}{2j} (e^{jwt} - e^{-jwt})$
• $\cos wt = \frac{1}{2} (e^{jwt} + e^{-jwt})$

于是

• $f(t) = \sin wt \rightarrow F(t) = \frac{w}{s^2+w^2}$

• $f(t) = \cos wt \rightarrow F(t) = \frac{s}{s^2+w^2}$

• $f(t) = \lim_{\epsilon \rightarrow 0} \frac{1}{\epsilon} \rightarrow F(t) = 1$

性质:

1. 位移定理: 乘上一个指数项 -> 加一个常数项
2. 微分定理: 做n阶微分 -> 乘上n阶项 (0初始条件)
3. 积分定理: 做n阶积分 -> 除以n阶项 (0初始条件)
4. 终值定理: 做无穷极限 -> 乘上s做0极限
5. 初值定理: 0初值 -> 乘上s 做无穷极限

性质0: 线性

$$L(af(t)) = aF(s)$$

$$L(af_1(t) + bf_2(t)) = aF_1(s) + bF_2(s) =$$

性质1: 时间平移

$$L(f(t-a)) = e^{-as}F(s)$$

性质2: 频率域平移

$$F(s+a) = L[f(t)e^{-at}]$$

性质3: 尺度变化

$$L[f(t/a)] = aF(as)$$

性质4: 微分性质

$$L[\frac{d}{dt}f(t)] = sF(s) - f(0)$$

推广得到

$$L[\frac{d^n}{dt^n}f(t)] = s^nF(s) - s^{n-1}f(0) - ... - sf^{(n-2)}(0) - f^{(n-1)}(0)$$

即, 时间域上的求导操作, 可以转换成频率域上的代数运算 $s \equiv \frac{d}{dt}$. 对于n阶导数, 需要其$0$阶导数到$n-1$阶导数的0点值

证明: 一阶导情况: 根据

$$\frac{d}{dt} [f(t) e^{-st}] = (\frac{d}{dt} f(t)) e^{-st} -s e^{-st} f(t)$$

代入积分式中即可.

推广可得到n阶导情况.

性质5 终值定理

$$\lim_{t\rightarrow \infty} f(t) = \lim_{s\rightarrow 0} sF(s)$$

需要:

• $f(t)$和 $df(t) / dt$ 存在拉普拉斯变换
• $F(s)$在虚轴上无极点, 在原点处无多重极点
• $\lim_{t\rightarrow \infty} f(t)$ 存在 (不存在时, 例如正弦函数时, 定理失效)

证明:
对于微分定理, 令s趋于0, 左右两边作变化得到

$$\lim _{s \rightarrow 0} L[\frac{d}{dt}f(t)] = \lim _{s \rightarrow 0} \int_{0}^{\infty} f'(t)e^{-st} dt = \int_{0}^{\infty} f'(t) dt = \lim _{t \rightarrow \infty} [f(t)] - f(0) = \lim _{s \rightarrow 0} [sF(s)] - f(0)$$

性质6 初值定理:

$$\lim_{t\rightarrow 0} f(t) = \lim_{s\rightarrow \infty} sF(s)$$

需要:

• $f(t)$和 $df(t) / dt$ 存在拉普拉斯变换
• $\lim_{s\rightarrow \infty} sF(t)$ 存在

TODO: 证明

对于微分定理, 令s趋于无穷, 左右两边作变化得到

$$\lim _{s \rightarrow \infty} L[\frac{d}{dt}f(t)] = \lim _{s \rightarrow \infty} \int_{0}^{\infty} f'(t)e^{-st} dt = 0 = \lim _{t \rightarrow \infty} [f(t)] - f(0) = \lim _{s \rightarrow \infty} [sF(s)] - f(0)$$

性质7 积分定理:

$$L(\int f(t)dt) = \frac{F(s)}{s} + \frac{f^{-1}(0)}{s}$$

其中, $f^{-1}(0) = \int_{-\infty}^{0}f(t)dt$是积分函数的初值.
$\int f(t)dt = \int_{-\infty}^{t}f(t)dt$

推广为

$$L[\int \int ...\int f(t) dt^n] = \frac{1}{s^n}F(s) + \frac{1}{s^n}f^{(-1)}(0) + ... + \frac{1}{s^2}f^{(-n+1)}(0) + \frac{1}{s}f^{(-n)}(0)$$

其他性质:

1. 线性
2. 时间平移 -> 频率域乘上指数
3. 频率域平移 -> 时间域乘上指数
4. 尺度变换: $L[f(\frac{t}{a})] = aF(as)$
5. 微分性质: $L(\frac{d}{dt} f(t)) = sF(s)-f(0)$. 于是, 在零初始条件下, 时间域求导运算变成了频率域代数运算 $s \equiv \frac{d}{dt}$ (求导算子等价于 s 算子)
6. 终值定理: 需要相应变换存在, 且 $F(s)$在虚轴上无极点, 在原点无多重极点. (根据微分定理证得. 因此需要导数的变换存在. )
7. 初值定理: 同样需要原函数和导数的变换, 以及极限存在.
8. 积分定理: 原函数积分再变换, 等于频率域函数除以一个s算子.

拉普拉斯反变换

通常有

$$F(s) = \frac{B(s)}{A(s)}$$

其中A, B为多项式.

此时可将A写为根式结合的形式, 从而将F(s)展开为部分分式.
然后进行分类讨论

1. F(s)只含有不同的实数极点
2. F(s)含有共轭复数极点
3. F(s)含有重极点

对于情况1, 将F(s)展开为分子只有常数的分式和, 其中分子称为留数. 从而得到拉普拉斯反变换的解.

对于情况2, 我们考虑共轭复数极点 $-p_1, -p_2$
于是有

$$F(s) (s+p_1)(s+p_2)|_{s = p_1, p_2} = A_1s + A_2|_{s = p_1, p_2}$$

其中左端的两个因式会被消掉.

于是就可以通过配凑的方法, 凑成正弦函数和余弦函数的 "分式平方"形式.