LearnLog

学习控制理论课程PPT的记录. 相关笔记会另开博客记录. 也可能不会开.

总结:

  1. 引入了传递函数模型. 它是微分方程精确解的一个近似.
  2. 引入了传递框图. 可以通过框图, 求解复杂系统的总传递函数.
  3. 引入信号流图模型和梅森公式, 构建起求解总传递函数的公式范式
  4. 引入MATLAB, 机械化求解系统的动态关系.

传递函数模型

对于微分方程的通式

a0dndtny(t)+a1dn−1dtn−1y(t)+...+an−1ddty(t)+any(t)=a_0 \frac{d^n}{dt^n}y(t) + a_1 \frac{d^{n-1}}{dt^{n-1}}y(t) + ... + a_{n-1} \frac{d}{dt}y(t) + a_n y(t) =

b0dmdtmr(t)+b1dm−1dtm−1r(t)+...+bm−1ddtr(t)+bmr(t)b_0 \frac{d^m}{dt^m}r(t) + b_1 \frac{d^{m-1}}{dt^{m-1}}r(t) + ... + b_{m-1} \frac{d}{dt}r(t) + b_m r(t)

于是零初始条件下有

(a0sn+a1sn−1+...+an−1s+an)Y(s)=(b0sm+b1sm−1+...+bm−1s+bm)R(s)(a_0 s^n + a_1 s^{n-1} + ... + a_{n-1}s + a_n) Y(s) = (b_0 s^m + b_1 s^{m-1} + ... + b_{m-1}s + b_m) R(s)

于是我们就得到

Y(s)=G(s)R(s)Y(s) = G(s)R(s)

其中G(s)称为传递函数. 它是将复杂分式吸收起来的结果. 是求解方程的半成品.

  1. 只适用于线性定常系统. 定义于0初始条件的情况下.
  2. 是复变量的有理分式函数, n≥mn\geq m, 各系数为实数
  3. 物理性质不同的系统, 传递函数可以相同.
  4. 表示的是线性定常函数自身的性质.
  5. 其拉普拉斯反变换是系统的脉冲响应. ( y(t)=g(t)∗δ(t)y(t) = g(t) * \delta (t)).∗*是卷积运算符.
  6. s=0s = 0时, 得到的 G(0)=KG(0) = K称为系统的放大系数 / 增益. (相当于微分方程中所以导数项都为0, 系统处于静态中)
  7. 分母位置的分式 N(s)N(s)为系统的特征分式, N(s)=0N(s) = 0称为特征方程, 它的根为特征根. 它的次数为系统的阶次.
  8. 特征根称为极点, 分子分式的根称为零点. 极点和零点完全取决于系统本身. 和输入输出没有关系. 极点决定系统的主要动态特性

(对于串联系统, 传递函数可以直接相乘得到. 类似复合函数求导. )

可将传递函数写为特定的分解形式
分解为6种因子. (分子0阶, 分子一阶, 分子二阶; 分母0阶, 分母一阶, 分母二阶. )

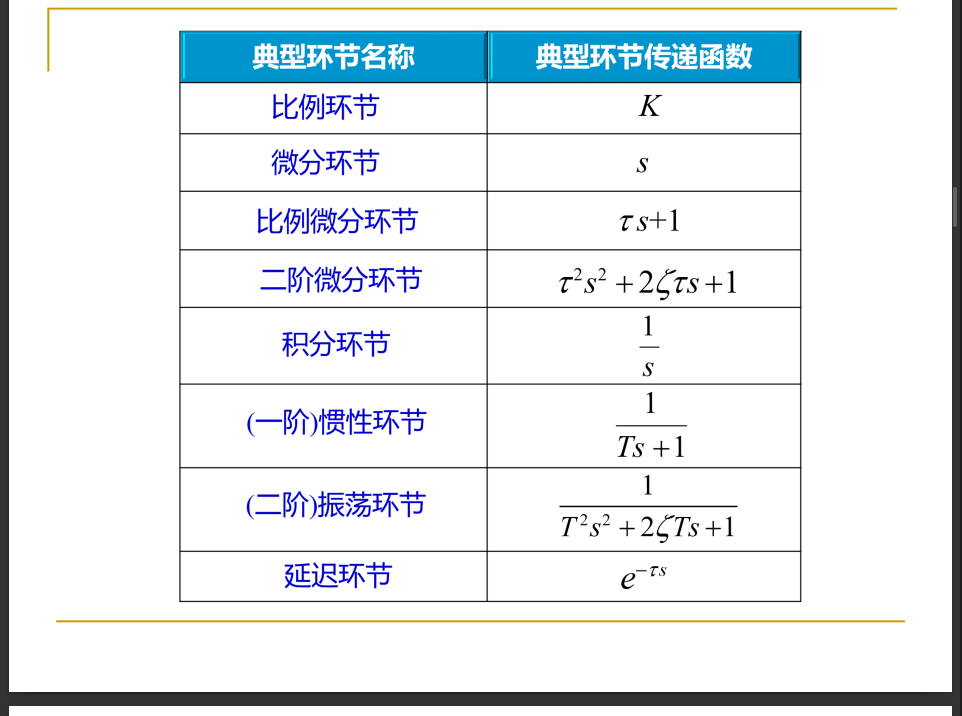
六种因子可称为6种环节. 他们共同作用, 导出了整个系统的性质.

  1. 比例环节, 又称放大环节. 特点: 输入输出成比例
  2. 比例微分环节: 时间域上添加了微分算子, 频率域上添加了一阶s算子. 特点: 系统输出与输入量本身有关, 还与输入量变化率有关.
  3. 二阶微分环节: 时间域添加了二阶微分, 频率域上添加了二阶s算子. 特点: 和输入的零一二阶导数均有关.
  4. 积分环节: 输出是输入的积分形式. 频率域上添加了 1/s 算子. 特点: 输出是输入的累积量
  5. 惯性环节: 输出具有延迟. 输入与输出, 输出的一阶微分有关. 频率域上是 1/(s + 1)的形式
  6. 二阶振荡环节: 输出带有振荡性质. 输入与输出, 输出的一二阶微分均有关.
  7. 延迟环节: 输出具有延迟. 前半段时间完全没有输出. 后半段时输出完全等于输入.

总结: 传递函数是微分方程模型的替代品, 求解方程的半成品. 它能够部分地描述出系统的各种性质. 基于传递函数的模型方便而简洁.

框图模型

在模糊的定性描述框图中, 引入定量的传递函数部分.

框图连接的性质
串联连接: 影响相乘
并联连接: 影响相加
反馈连接: 联立方程求解, 可得到系统的闭环传递函数.

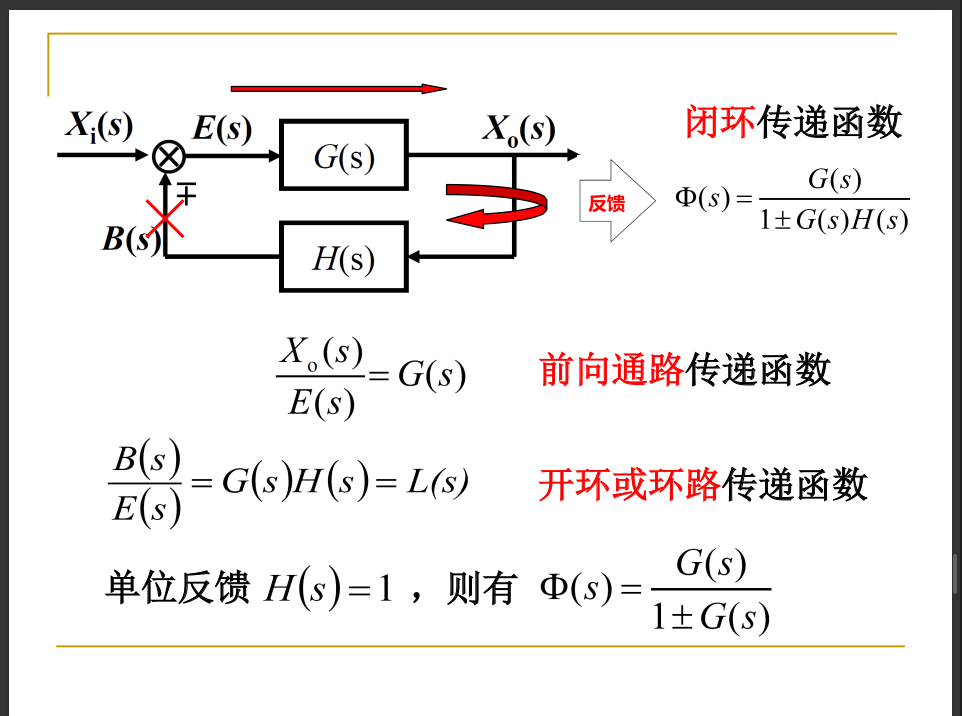
框图的等效变换:
比较点前移 / 后移的等效性
引出点前移 / 后移的等效性

用框图求系统传递函数:

利用等效变换法则, 移动比较点和引出点, 消去交叉回路, 变成简单回路

  • 考虑扰动的闭环控制系统: 在前向通路中加入扰动
  • 分别求解无扰动传递函数; 仅有扰动的传递函数. 从而得到叠加系统的总输出. (同时也可求解偏差的传递函数. )

信号流图模型

是一种特殊的有向图模型. 根据信号流图模型和梅森公式, 可以方便地求解出系统的传递函数.

  • 节点: 表示变量或信号. 值为所有进入信号之和.

  • 支路: 相当于边. 用支路增益表示两个变量的因果关系.

  • 输入节点 / 源节点: 只有输出的节点

  • 输出节点 / 汇点: 只有输入的节点

  • 混合节点: 有输入也有输出的节点. 从混合节点可以引出汇点

  • 框图模型与信号流图模型一一对应. (框图中框 / 点表示转移函数; 信号流图中边表示转移函数)

  • 前向通路: 输入 -> 输出. 所有节点至多出现一次

  • 回路: 某节点 -> 自身. 所有节点至多出现一次

  • 不接触回路: 互相直接没有公共节点

绘制: 1.从框图到信号流图 2. 从方程式到信号流图.

梅森公式

P=1△∑kPk△kP = \frac{1}{\triangle} \sum_k P_k \triangle _k

其中

  • P: 系统总的传递函数
  • △\triangle: 信号流图的特征式
  • PkP_k: 第k条前向通路的传递函数
  • △k\triangle_k: 第k条前向通路的余因子.

具体计算方法:

MATLAB实现系统数学模型

一. 多项式: MATLAB中用系数行向量表示

  • value = polyval(p, -5) 求多项式值
  • r = roots(p) 求解多项式根
  • p = poly(r) 根据根重构多项式

二. 用传递函数描述
sys = tf(num, den)
描述转移函数. 其中num为分子多项式, den为分母多项式

z = zero(sys), p = pole(sys). 计算转移函数的零点, 极点
pzmap(sys) 绘制零-极点分布图

三. 零-极-增益模型描述
sys = zpk(z, p, k) 分别为零点, 极点, 增益系数.

四. 传递函数与零-极-增益模型互相转换
[z, p, k] = tf2zp(num, den)
[num, den] = zp2tf(z, p, k)

五. 多项式相乘
conv(den1, den2)

六. 计算系统传递函数
串联: sys = series(sys1, sys2)
并联: sys = parallel(sys1, sys2)
反馈: sys = feedback(sys1, sys2, sign)
单位反馈: sys = cloop(sys1, -1) 相当于 sys = feedback(sys1, [-1], sign)

七. 部分分式展开(求解反拉普拉斯变换)
[r, p, k] = residue(num, den)
其中r为留数, p为极点, k为余项多项式

[num, den] = residue(r, p, k). 将部分分式合并

八. 零-极点对消
sys = minreal(sys)

九. 计算系统的单位阶跃响应
[y, T] = step(sys, t)

十. 从构建系统到计算其单位阶跃响应

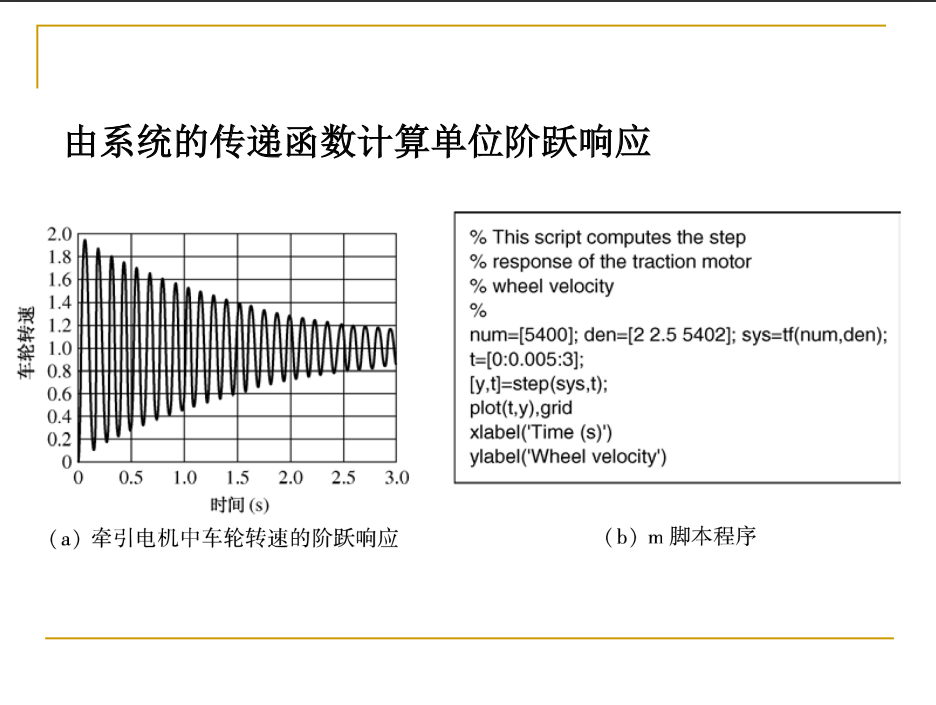
总结:

目标: 实现对变量的自动控制
途径: 先分析系统特性, 构建系统的数学模型, 然后进行设计

数学模型:

  • 微分方程模型 -> 传递函数模型 -> 框图模型 -> 信号流图模型 -> * 状态空间模型

  • 拉普拉斯变换: 将函数从时域上的微分方程变换至复数域上的传递函数.

  • 性质: 位移定理, 微分定理, 积分定理, 终值定理, 初值定理

  • 常见函数的变换: 指数函数, 阶跃函数, 斜坡函数, 幂函数, 正弦函数, 余弦函数, 单位脉冲函数

  • 传递函数定义: 零初始条件下, 输出拉普拉斯变换与输出拉普拉斯变换的比值

  • 典型传递函数: 比例环节, 微分环节, 比例微分环节, 二阶微分环节, 积分环节, 一阶惯性环节, 二阶振荡环节, 延迟环节

  • 框图模型, 信号流图模型

  • 梅森公式

backtop