基于上海交通大学强化学习课程系列课程学习RL的笔记.
SJTU RL Course (wnzhang.net)
前面我们基于格子世界, 讨论了离散状态和离散动作. 现在, 我们引入神经网络, 开始探索连续的使世界.
参数化价值函数
- 之前, 我们一直在维护一个大型的状态值函数 / 状态-动作函数表
- 当空间十分大时, 维护这个表带来困难.
- 解决方案: 分桶 / 构建参数化的值函数估计
离散化/分桶
优点: 直观简洁, 高效, 很多问题下效果较好
缺点: 表达的可能过于粗略; 需要认为的确定桶的大小; 维度灾难
参数化值函数近似
通过参数构建函数, 可以泛化到没见过的状态
主要形式:
- 函数近似, 如线性模型, 神经网络, 决策树, 最近邻, 傅立叶/小波基底等
- 可微函数: 如线性模型和神经网络
- 对于非稳态, 非独立同分布的数据, 参数化模型比树模型更合适
基于随机梯度下降 SGD的值函数近似
- 对于每一个样本的梯度, 它是实际的"期望梯度"的随机采样
- 根据这个采样结果进行随机梯度下降. 期望上逼近想要的方向.
价值函数近似算法
我们考虑
其近似目标是实际上的价值函数Q.
对于
可以得到梯度为
于是, 只要我们得到近似的策略函数的导数, 以及实际需要逼近的目标函数 , 即可完成SGD.

其中, 若用 作为逼近目标, 我们就得到MC的算法; 若用 作为目标, 我们就得到 TD(0)算法.

上面的更新方式都是拟合值函数的 策略迭代方法. 我们在拟合好值函数后, 进行策略提升.
策略梯度
基于策略的RL
我们将策略也进行参数化, 并显式地进行相关考虑
优点: 收敛性质更好; 高维度和连续的动作空间中更有效; 能够学习随机策略
缺点: 通常会收敛到局部最优; 评估策略不够有效, 方差较大
其中, 由于要求解"期望的导数"是不太容易的, 于是我们用一个trick将其进行变换
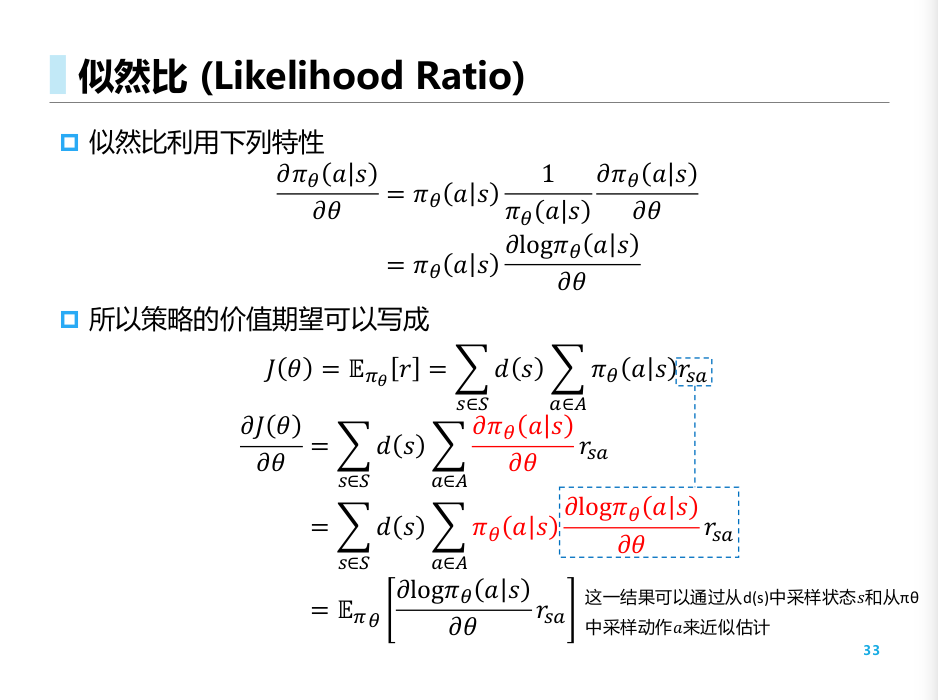

详细的证明可参考
https://hrl.boyuai.com/chapter/2/策略梯度算法/
以及PPT附录 (https://wnzhang.net/teaching/sjtu-rl-2024/slides/rl-proofs.pdf). 其实还是没什么trick的, 只是根据定义一步一步推导.
于是, 根据策略梯度定理, 我们只要求出对数策略的梯度, 就能够得到最终的下降方向.
REINFORCE
按照策略梯度定理, 将G_t作为拟合目标, 我们得到MC策略梯度算法(拟合Q函数的算法):

Softmax 随机策略
我们考虑根据 得到的随机性策略. 其中f可以是某种打分函数.
其对数似然的梯度可以根据链式法则得到.
Actor-Critic
REINFORCE基于MC, 所以存在相应的缺点
- 需要任务有终止态
- 低数据利用率
- 高训练方差(整个轨迹过长, 方差连乘累计)
AC思想: 不直接使用 , 而是建立一个拟合的价值函数 , 通过让出偏差来减小方差

Critic: 近似目标为当前Actor 的动作价值
Actor: 近似目标为当前Critic 下的最优策略.
A2C: 通过定义基线函数, 使得差的动作在神经网络中的输出被减小(之前所有的输出都会一直增加, 若奖励为正, 只是幅度不同)
基线函数可以通过状态值函数来拟合得到. (等式变换)
其中期望通过不断采样来近似得到.

