[RL] 第八讲: 深度策略梯度

基于上海交通大学强化学习课程系列课程学习RL的笔记.
SJTU RL Course (wnzhang.net)

前面讲的DQNs和DPGs要么是基于价值的方法, 要么是基于确定性策略的方法. 这里我们讨论基于随机策略的方法.

---

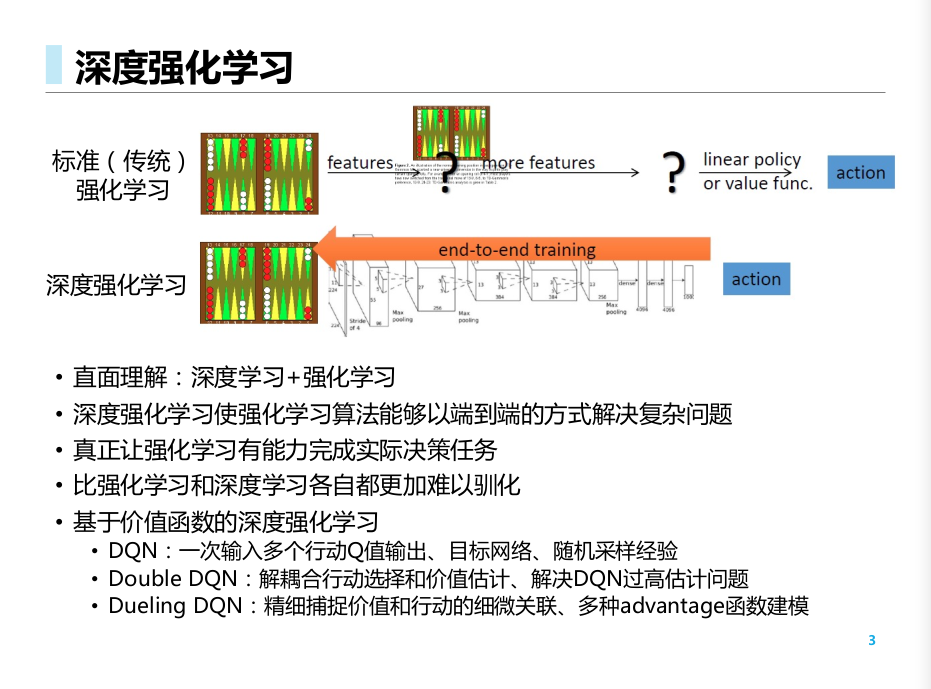
基于神经网络的策略梯度

策略梯度定理:

$$\frac{\partial J(\theta)}{\partial\theta} = E_{\pi_\theta}[\frac{\partial \log \pi_{\theta}(a|s)}{\partial\theta} Q^{\pi_{\theta}} (s, a)]$$

将需要求解的误差梯度转换为了策略的对数梯度, 以及价值函数的值.

这个定理对于多种J的定义都是成立的.

策略学习与Q学习的对比

• Q学习算法学习一个参数函数Q.
  • 优化目标为最小化TD error (通过bellman最优方程, 逼近最优价值函数)
  • 更新方程为

$$\theta \leftarrow \theta - \alpha \frac{\partial J(\theta)}{\partial\theta} = \theta + \alpha E_{\pi'}[ (r_t + \lambda \max_{a'} Q_{\theta '}(s_{t+1}, a') - Q_{\theta}(s_t, a_t))\frac{\partial Q_{\theta}(s_t, a_t)}{\partial\theta}]$$

• 策略梯度学习一个参数表示的策略pi
  • 优化目标直接为策略的价值(比Q学习更直接, 直接逼近最优策略)
  • 更新方程为

$$\theta \leftarrow \theta + \alpha \frac{\partial J(\theta)}{\partial\theta} = \theta + \alpha E_{\pi_{\theta}} [\frac{\partial \log \pi_{\theta}(s |a)}{\partial\theta} A^{\pi_{\theta}}(s, a)]$$

A3C

AC: 建立了一个可训练的值函数, 之后采用类似TD(0)的方法进行训练.
A2C: 通过基线函数, 标准化Critic的打分.
A3C: 异步A2C方法.Asynchronous Advantage Actor Critic

在普通A2C 方法中引入了异步并行训练. 训练时, 不再是单步TD, 而是k步TD

Volodymyr Mnih et al. Asynchronous Methods for Deep Reinforcement Learning. NIPS 2016.

• A3C的并行设置使得我们能够用多个性能较差的设备(如CPU) 达到和高性能设备(如GPU) 一样的效果

信任区域策略优化 TRPO

初衷

• 策略梯度算法(如 REINFORCE)需要确定一个更新步长 $\alpha$, 而这在实际过程中难以确定
  • 数据分布会随着策略更新而改变
  • 较差的步长会导致采集到的数据变坏, 进而陷入恶性循环

“OPTIMIZING EXPECTATIONS: FROM DEEP REINFORCEMENT LEARNING TO STOCHASTIC
COMPUTATION GRAPHS”，John Schulman. (2016)

TRPO

我们先考虑"更新步长的概念", 即, 策略每次更新, 其 $J(\theta)$变化不能过大.

推导, 得到优化目标的优化量公式.

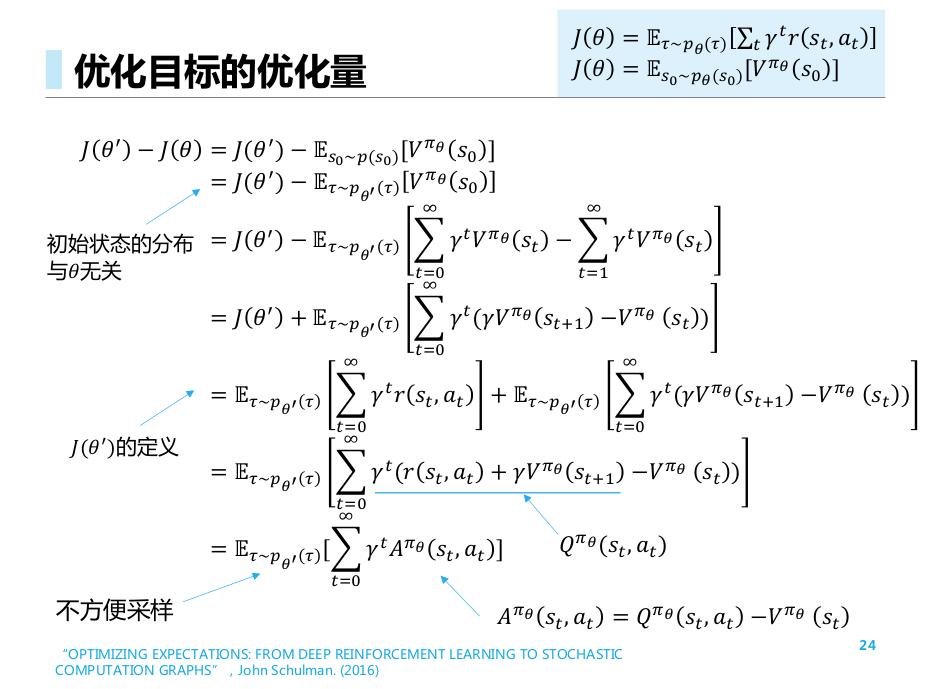
从原始出发, 先引入同一个分布, 再通过配凑得到Bellman等式的形式, 然后凑成 $A^{\pi_{\theta}}$的求和期望形式.
之后, 由于原来的分布不方便采样, 我们进行重要性采样, 得到新的分布形式

此处进行了一次近似操作, 即认为两次更新之间, 关于 $s_t$的分布是变化不大的.

“OPTIMIZING EXPECTATIONS: FROM DEEP REINFORCEMENT LEARNING TO STOCHASTIC
COMPUTATION GRAPHS”，John Schulman. (2016)

http://rail.eecs.berkeley.edu/deeprlcourse/static/slides/lec-9.pdf

单调性保证

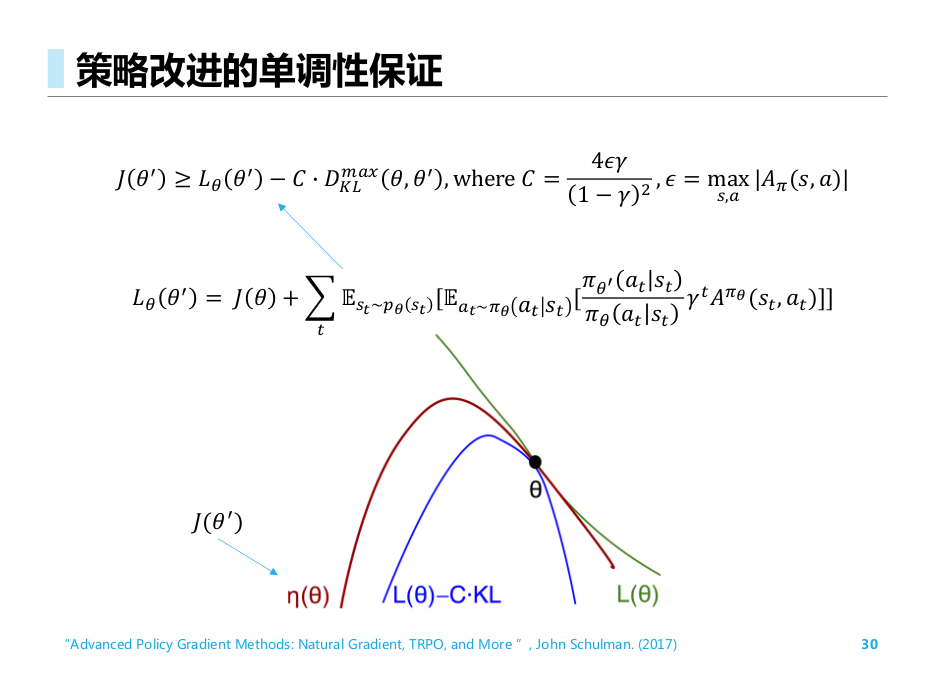
“Advanced Policy Gradient Methods: Natural Gradient, TRPO, and More ”, John Schulman. (2017)

TRPO的不足:

• 近似带来的误差
• 求解约束优化问题的困难.

PPO 算法:
Proximal Policy Optimization Algorithms,
John Schulman, et al. (2017)

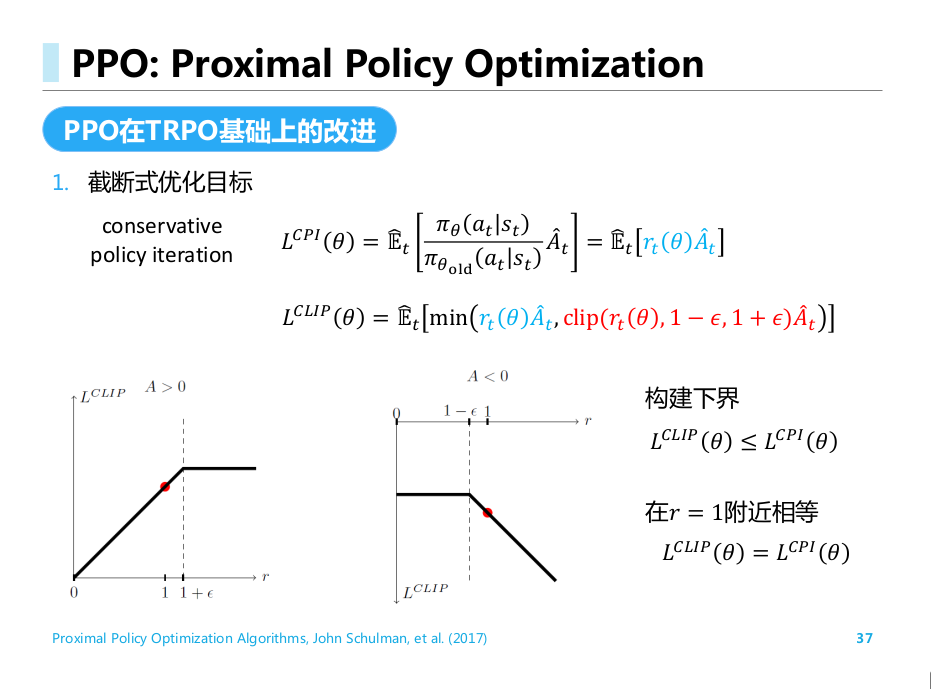
PPO

• TRPO采用KL散度约束策略更新的幅度. (重要性比例带来大方差; 求解约束优化问题困难. )
• PPO引入截断式优化目标; 优势函数中引入多步时序差分; 自适应KL惩罚项参数

总结

数学内容非常多, 涉及到一些论文. 有时间把数学原理推一推, 论文看一看, 再写个自己的库实现.
现在先往后推进吧.