LearnLog

学习Automata PPT的记录. 相关笔记会另开博客记录. 也可能不会开.

  • PDA是等价于CFG的自动机. (关于互相转换的构造过程. )
  • 只有非确定性PDA能够包含所有CFL. (确定性PDA比较弱, 而且两种生成方式的结果有区别. )
  • 大部分编程语言可以通过 Deterministic PDA 描述. (满足Prefix Property?)

PDA Intuition

  • 引入了一个栈
  • PDA的行为由当前状态, 当前输入, 栈顶元素共同决定

对于每个动作, PDA可以

  1. 改变状态, 同时
  2. 将栈顶符号替换为任意数量的符号 (一次pop和任意次push)

形式化的, PDA可以通过七元组表示

PDA=<Q,Σ,Γ,δ,q0,Z0,F>PDA = <Q, \Sigma, \Gamma, \delta, q_0, Z_0, F>

  1. 一个有限状态集合
  2. 输入字母表
  3. 栈字母表
  4. 转移函数
  5. 起始状态
  6. 起始符号
  7. 有穷终止集合

对于转移函数, δ(q,a,Z)\delta(q, a, Z) is a set of zero or more actions of the form (p,Z′)(p, Z')

  • 接受当前状态, 当前输入, 以及栈顶元素
  • 返回下一个状态以及一系列栈中的元素 (类似NFA, 有多个动作可以同时进行. )

对于每一个输入 aa, PDA会

  1. 转移状态
  2. 将a从input 移除 (a可以是空字符)
  3. 将栈顶元素进行替换

用栈来存储信息: 表示 0n1n0^n1^n

Instantaneous Descriptions (ID)

A ID is a triple (q, w, X), where:

  1. q is the current state
  2. w is the remaining input
  3. X is the stack contents, top at the left

类似广义的状态.

广义状态转移函数 “Goes-To” Relation

  1. ID I can become ID J in one move of the PDA: I⊢JI \vdash J
  2. Extend Goes-To : I⊢∗JI \vdash^* J. 任意次转移

TH 1: Given a PDA P, if (q,x,Z)⊢(p,y,Z′)(q, x, Z) \vdash (p, y, Z'), for all the string w∈Σ∗w \in \Sigma ^* and all string γ∈Γ∗\gamma \in \Gamma ^*, we have (q,xw,Zγ)⊢(p,yw,Z′γ)(q, xw, Z\gamma) \vdash (p, yw, Z'\gamma)

类似的"反面"定理:

TH2: Given a PDA P, if (q,xw,Z)⊢(p,yw,Z′)(q, xw, Z) \vdash (p, yw, Z'), we have (q,x,Z)⊢(p,y,Z′)(q, x, Z) \vdash (p, y, Z')

注意, 这并不是TH1的直接反面. 因为 γ\gamma可能被用到, 与输入不同(并不完全是线性遍历)

Language of a PDA

The common way is by final state

L(P)={w∣(q0,w,Z0)⊢∗(f,ϵ,α)}L(P) = \{w | (q_0, w, Z_0) \vdash ^* (f, \epsilon, \alpha)\}

只关心状态是否为终止态, 字符串是否读完, 对栈中的内容并不关心

Another language defined by the same PDA is by empty stack.

N(P)={w∣(q0,w,Z0)⊢∗(q,ϵ,ϵ)}N(P) = \{w| (q_0, w, Z_0) \vdash ^* (q, \epsilon, \epsilon)\}

只关心栈中是否是空, 字符串是否读完, 对状态并不关心

Equivalence of Language Definitions

  1. If L=L(P)L = L(P), then there is another PDA P′P' such that L=N(P′)L = N(P')
  2. If L=N(P)L = N(P), then there is another PDA P′′P'' such that L=L(P′′)L = L(P'')

构造性地证明定理的正确性
Proof:
对于L(P)−>N(P′)L(P) -> N(P')

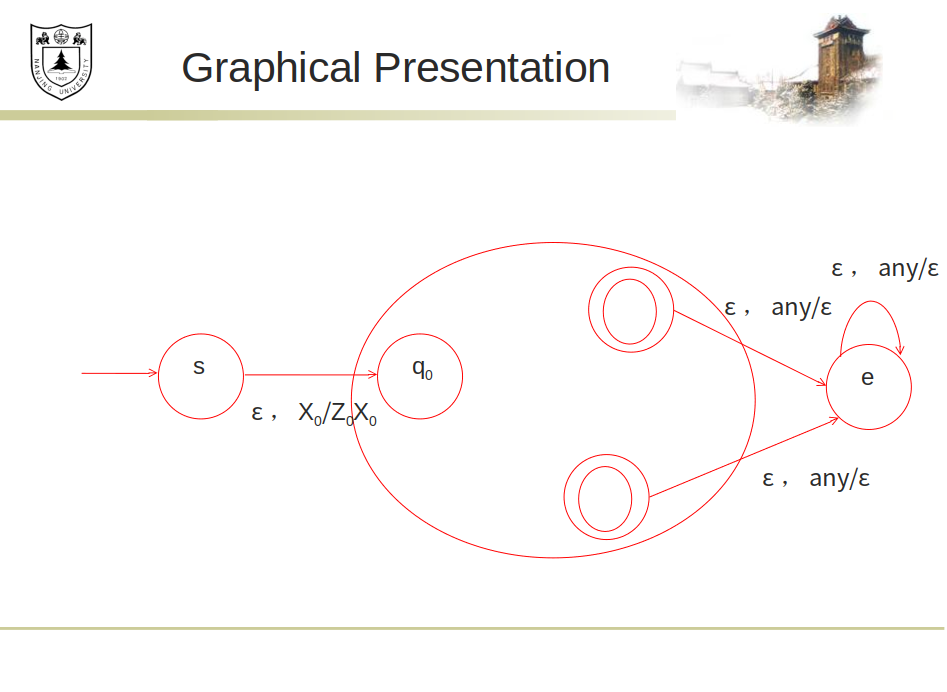
对于新的PDA, 为了防止它的栈意外地空了, 添加一个守卫元素 X0X_0. (原本栈空了且不在终止态时, 不应该被接收; 但是倘若不添加守卫元素, 它就会在新的N(P)中被接收. )

  1. 引入一个新的起始状态 ss 和一个 “最终状态” ee.
  2. 添加转移函数为 δ(s,ϵ,X0)={(q0,Z0X0)}\delta (s, \epsilon, X_0) = \{(q_0, Z_0X_0)\}
  3. 添加{(e,ϵ)}\{(e,\epsilon)\} 到 δ(f,ϵ,X)\delta (f, \epsilon, X), 对于任意的 XX
  4. 添加 δ(e,ϵ,X)={(e,ϵ)}\delta (e, \epsilon, X) = \{(e, \epsilon)\}

一头一尾添加一个"转接口". 其实感觉尾巴的转接口有点怪了. 应该设置成先把所有终止态上的东西转移成 X0X_0, 然后再把X0X_0统一转换成空. 这样比较自然一点.
或者直接删掉e上的转换也可以.

对于N(P)−>L(P′′)N(P) -> L(P'')

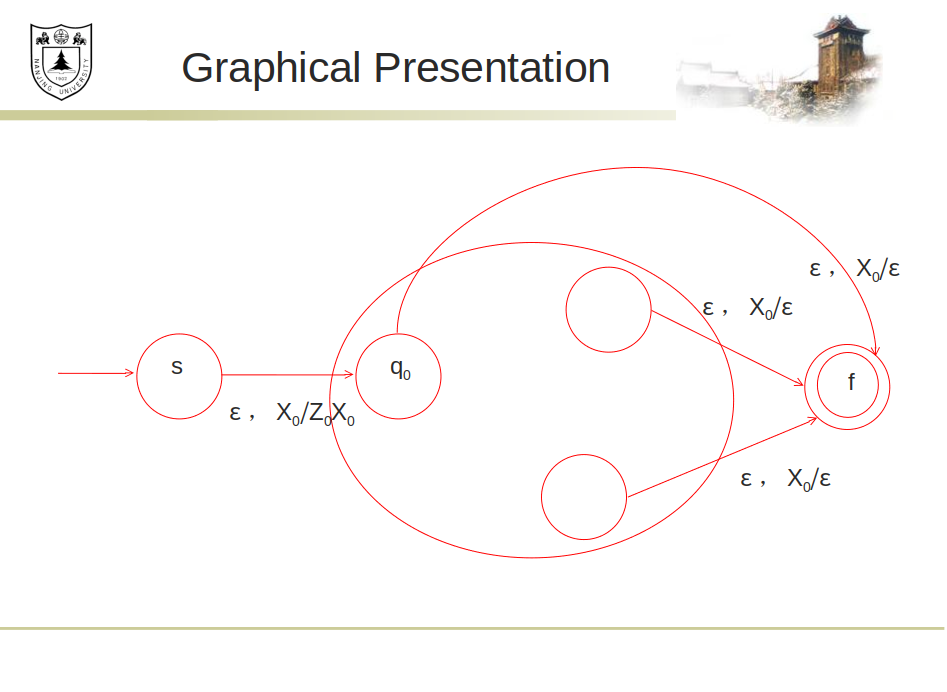
对于新的PDA, 为了捕捉栈为空的情况, 添加一个标记元素 X0X_0.

  1. 引入一个新的起始状态 ss 和一个终止状态 ff.
  2. 添加转移函数为 δ(s,ϵ,X0)={(q0,Z0X0)}\delta (s, \epsilon, X_0) = \{(q_0, Z_0X_0)\}
  3. 添加δ(f,ϵ,X0)={(f,ϵ)}\delta (f, \epsilon, X_0) = \{(f, \epsilon)\}, 对于任意的 XX

一头一尾添加一个"转接口"

Example: 构建 if-else 语法的CFL.
通过N(P)N(P)的方式构建是显然的(记录if的个数, 然后让else与之相匹配).
可以将N(P)N(P)的PDA改写成 L(P)L(P)的PDA

改写成Deterministic PDA’s

要求: 对于每个状态, 动作需要有且只有一个 (不能为空, 也不能有多个)

  • 动作可以包含空字符作为输入.
  • 且只有在"无路可走"的时候, 通过空字符进行移动才能被允许.

对于DPDA和 NPDA

NPDA is more powerful than DPDA

Ex:

  1. 考虑语言wwRww^R, 例如{0m110m}\{0^m110^m\}. 它只接收m个0的情况.
  2. 同时, 我们考虑 N(P)N(P)
  3. 那么, 它在接收到 0m110m0^m110^m时, 栈一定会是空的. 此时若字符串终止, 则它将这个字符串接受.
  4. 这时, 如果它又接收到串 0m110m0^m110^m, 它应当接受整个字符串 0m110m0m110m0^m110^m0^m110^m.
  5. 这时, 如果它又接收到串 0n110n0^n110^n, 它应当拒绝整个字符串 0m110m0n110n0^m110^m0^n110^n.
  6. 这个时候, 因为栈已经是空的了(DPDA退化为DFA), 所以DPDA无法判断m≠nm \neq n

这个证明过程好像没那么精确. 因为N(DPDA) 具有 prefix property, 所以直接可以得到反例.

假如采用final states定义呢?
此时不考虑栈的时候, DPDA退化为DFA. 假设有这样的DPDA.
对于任意回文字符串 ww, 我们有 δ∗(q0,w,Z0)=(f,α)\delta ^*(q_0, w, Z_0) = (f, \alpha), 其中 α\alpha可以与输入相关, 也可以无关.
此时, 我们再次输入ww, 那么就会有 δ∗(f,w,α)=(f′,β)\delta ^*(f, w, \alpha) = (f', \beta)
输入一个与ww不同的回文串w′w', 就会有 δ∗(f,w′,α)=(q,γ)\delta ^*(f, w', \alpha) = (q, \gamma), 且 qq 不为接收态.

思路: 假设有这样的DPDA, 构造反例. "信息有限"的角度考虑.

  1. 由于转移是确定性的. 所以只考虑栈顶元素的情况下, 一定存在这样的情况, 此时 (q0,w,Z0)⊢∗(q,ϵ,α),(q0,w′,Z0)⊢∗(q,ϵ,β)(q_0, w, Z_0) \vdash^* (q, \epsilon, \alpha), (q_0, w', Z_0) \vdash^* (q, \epsilon, \beta). 其中 w,w′w, w'为两个不同的字符串, qq为同一个状态, α,β\alpha, \beta的栈顶元素相同.
  2. 此时, 若输入同一个字符串, 它们后续的转移过程都是一样的, 因为栈顶元素的状态是一致的.
  3. 但是, wwRww^R需要被接受, 而 w′wRw'w^R需要被拒绝. 这是不可能的. 产生矛盾.

所以, 两种定义下, NPDA都强于DPDA.

但是DPDA可以用于表示 wcwRwcw^R. (因为此时明确给出了一个界限c. 如果没有这个界限c, 我们就只能借助非确定性的力量来"猜测")

  1. 当没有遇见c的时候, push
  2. 否则, pop

TH: If L is a regular language, there exists a DPDA P, such that L=L(P)L = L(P)
即, L(P)定义的情况下, DPDA的表达力不弱于RE (因为采用final states定义的前提下, 它是推广的DFA, 当栈始终不变时, 它退化成普通的DFA)

这个定理中, DPDA的语言通过 final states定义. 如果是通过 N(P)N(P)定义呢? 这时情况就会发生变化…

Ex: 考虑 {0}∗\{0\}^*. 它可以用RE表示. 但是不存在DPDA, 使得L=N(P)L = N(P). (通过反证法可以证明)

采用empty stack 定义时, 若 w∈N(P)w \in N(P), 则对任意w′w', ww′ww'都不属于 N(P)N(P)
换言之, L(DPDA)L(DPDA)满足 prefix property性质, 即不存在两个串属于L, 使得一个串是另一个串的前缀.
这么看来DPDA采用empty stack时非常弱啊…

DPDA 的L语言与N语言的关系

Theorem 6.19:
A language LL is N(P)N (P) for some DPDA PP if and only if LL has
the prefix property and LL is L(P0)L(P_0) for some DPDA P0P_0 .

即, 在prefix property的前提下, L(P)∩PP=N(P)L(P) \cap PP = N(P)

L(P)>N(P)L(P) > N(P)

Prove:
假设对于语言 LL, 满足前置码的性质, 同时 L=L(P)L = L(P). 那么构造性地给出一个 N(P0)N(P_0):
2. 添加一个转接头, 负责加入守卫元素, 避免栈为空时, 错误把字符串接收了. (对于不该接收的状态, 如 (q,ϵ,ϵ)(q, \epsilon, \epsilon), 防止栈为空)
3. 对于所有 (f,ϵ,α)(f, \epsilon, \alpha), 它们转移到 (f,ϵ)(f, \epsilon). (这一点是由前置码保证的. 前置码告诉我们在原本的P中, (f,x,α)=∅(f, x, \alpha) = \emptyset) (对于应该接收的字符, 强制令栈为空)

假设对于语言 LL, 有一个 N(P0)N(P_0), 下面构造性地给出一个 L(P)L(P), 同时证明L满足前置性(显然):

  1. 添加一个转接头, 负责加入守卫元素.
  2. 在栈为空(只剩下守卫元素)且字符串为空时, 会转移到终止状态e (将应该接收的字符串接收)
    证毕.

于是我们有

L(NPDA)=N(NPDA)>L(DPDA)>N(DPDA)L(NPDA) = N(NPDA) > L(DPDA) > N(DPDA)

且

L(DPDA)>=L(RE)   (因为L(DPDA)可以退化成DFA)L(DPDA) >= L(RE) \ \ \ \text {(因为L(DPDA)可以退化成DFA)}

同时, 有的 L(RE)L(RE)无法用 N(DPDA)N(DPDA) 表达, 有的 N(DPDA)N(DPDA) 也无法用 L(RE)L(RE) 表达.

证明: 有的N(DPDA)N(DPDA) 不存在于 L(RE)L(RE) 中.
考虑前置码. 它从2位二进制开始, 其中一半用来表示, 另一半用来扩展.
例如, 00, 10用于表示, 01, 11衍生出 010, 110, 用于表示, 剩下的011, 111继续衍生.
此时, 所有编码的最后一个数为0. 且长度大于等于2.
发现它不能用RE表示, 但是可以用N(DPDA)N(DPDA)表示. (用TH6.19容易得到)

DPDA and Ambiguity

对于DPDA表示的语言L=L(P)L = L(P), 它一定有一个非二义性的语法.

但是, 非二义性的语法不一定能由DPDA来表达的. (可能只能用CFG / NPDA表达)

Ex: wwRww^R 可以用CFG : S -> 0S0 | 1S1 | epsilon来表示. 这是非二义性的语法, 同时不能用DPDA表达. (这不是显然吗. 非二义性又不是DPDA独有的性质. )

总结: DPDA表达的语言是CFG表达语言的一个子集. 这个子集具有特殊的性质, 即, 一定存在一个非二义性的CFG来表达它.
但是, 对于存在非二义性CFG的语言, 它不一定能用DFDA表达. 因此箭头是单向的.

Equivalenve of PDA, CFG

  1. PDA和CFG是等价的
    • 他们表示的是同一族语言: CFL / Context Free Languages
    • 就好像RE, DFA, NFAs表示的是同一族语言: Regular Languages
  2. 证明某个语言是CFL时, PDA很好用(例如, 对于括号平衡语言的证明)

CFG -> PDA
我们首先有 L=L(G)L = L(G), 下面需要构造一个 PP, 使得 N(P)=LN(P) = L. (由于是非确定性PDA, 因此怎么样生成语言并不重要. )
构造过程: 对于P,

  • 它只有一个状态
  • 它的输入符号是G的终止符
  • 它的栈符号是G的所有符号
  • 它的起始符号是G的起始符.

工作过程: 从起始符开始, 不断接收一连串终止符的输入, 根据CFG的 production来完成栈的维护, 并最终将栈清空(如果输入的字符串可接受).

At each step, P represents some left-sentential form (step for a leftmost derivation)

  1. δ(q,a,a)=(q,ϵ)\delta(q, a, a) = (q, \epsilon). 若输入的符号和栈顶符号都为终止符, 将终止符弹出. (不改变LSF)
  2. δ(q,ϵ,A)∪=(q,α)\delta(q, \epsilon, A) \cup= (q, \alpha), 如果 A−>αA ->\alpha 在production中. (对于栈顶元素, 猜测每一种生成方式)

给定上面的结构后, 证明 (q,wx,S)⊢∗(q,x,α)(q, wx, S) \vdash ^* (q, x, \alpha) for any x, if and only if S=>lm∗wαS => ^*_{lm} w \alpha
归纳证明:
only if: 对左边的生成步数做归纳. 当步数为0, 有S=αS = \alpha, w=ϵw = \epsilon, 显然. 然后做链条. 链条时根据两个Rule, 分两种情况讨论.
if: 对右边, 左递推的生成过程步数做归纳. 和only if 的过程类似.

通过上面的证明, 我们令它的一个特殊情况, 就可以迅速得到 CFG与PDA的等价性. 于是, 我们证明了, CFG能够转换为等价的PDA

PDA -> CFG

虽然添加元素的数量是任意的, 但是每次弹出元素时, 至多只能弹出一个.

因此, 我们令G有这样一个变量 [pXq], 如果有一个cause P, 令PDA恰好从p 转移到了q, 且只弹出了元素 X.
同时, 在进行P的过程中, 它永远不会 get below this X (如果我们考虑的是某种"最小操作集")

显然对于起始元素Z_0和 w∈N(P)w \in N(P), 它能生成一个变量 [p_0 Z_0 q]
对于栈的元素集合, 它能够相应地生成一个变量和对应的字符串集合 (因为它如果想接收一个字符串, 那么它总要被弹出. )

那么显然, G的变量[pXq]会且只会生成满足下面式子的符号

(p,w,X)⊢∗(q,ϵ,ϵ)(p, w, X) \vdash^* (q, \epsilon, \epsilon)

Production of G:
可以递归式地定义. 从状态p开始, 栈顶元素为X, 不断接收输入直到X恰好被弹出. 此时得到production

先考虑简单的情况:
case 1: 如果 (q,ϵ)∈δ(p,a,X)(q, \epsilon) \in \delta(p, a, X), 那么[pXq] -> a. a可以为空
case 2: 如果 (r,Y)∈δ(p,a,X)(r, Y) \in \delta(p, a, X), 那么[pXq] -> a[rYq].
case 3: 如果 (r,YZ)∈δ(p,a,X)(r, YZ) \in \delta(p, a, X), 那么[pXq] -> a[rYs][sZq], 对于所有的状态 s . 因此, 生成了一族productions.

对于一般的生成式:
考虑包含在 δ(p,a,X)\delta(p, a, X)中的式子 (r,Y1,...,Yk)(r, Y_1, ..., Y_k). 对于 k≥3k\geq 3 (0, 1, 2的情况已经讨论)
生成如下的一族productions:

[pXq]−>a[rY1s1][s1Y2s2]...[sk−2Yk−1sk−1][sk−1Ykq][pXq] -> a[rY_1s_1][s_1Y_2s_2]...[s_{k-2}Y_{k-1}s_{k-1}][s_{k-1}Y_{k}q]

于是, 根据上面两个构造得到的结构, 可以证明 (q0,w,Z0)⊢∗(p,ϵ,ϵ)(q_0, w, Z_0) \vdash ^* (p, \epsilon, \epsilon) if and only if [q0Z0p]=>∗w[q_0Z_0 p] => ^* w.

此处, p可以是任意状态, 所以和起始符号组合也得到一系列起始变量.

因此, 添加一个起始变量将这些状态吸收:

S−>[q0Z0p]S -> [q_0Z_0p]

backtop