[ControlSystem] Ch5 控制系统的性能

学习控制理论课程PPT的记录. 相关笔记会另开博客记录. 也可能不会开.

分析性能时, 我们主要分析二阶系统的时域响应性能. 性能指标为:

• 上升时间 $t_r$
• 峰值时间 $t_p$
• 调节时间 $t_s$
• 超调量 $P.O.$
• 震荡次数 Oscillation Number

控制系统的性能

回顾: 控制系统的数学解析:

$$Y(s) = G(s)R(s), y(t)=L^{-1}(Y(s))$$

数学式很强大, 但是还不够. 我们需要分析系统是否足够"快 , 准, 稳", 即

• 分析控制系统的性能 CH5
• 分析控制系统的稳定性 CH6

---

时域响应概述

考虑一个闭环控制系统, 我们的目标是

$$y(t) = r(t)$$

但是, 随着r的变化, y与r的误差往往不能保持为0, 而是会不断抖动.

此时, 我们分析系统的时域响应:

• 系统在输入信号的作用下, 输出随时间变化的过程
• 直观反映系统性能
• $y(t)=L^{-1}(Y(s))$

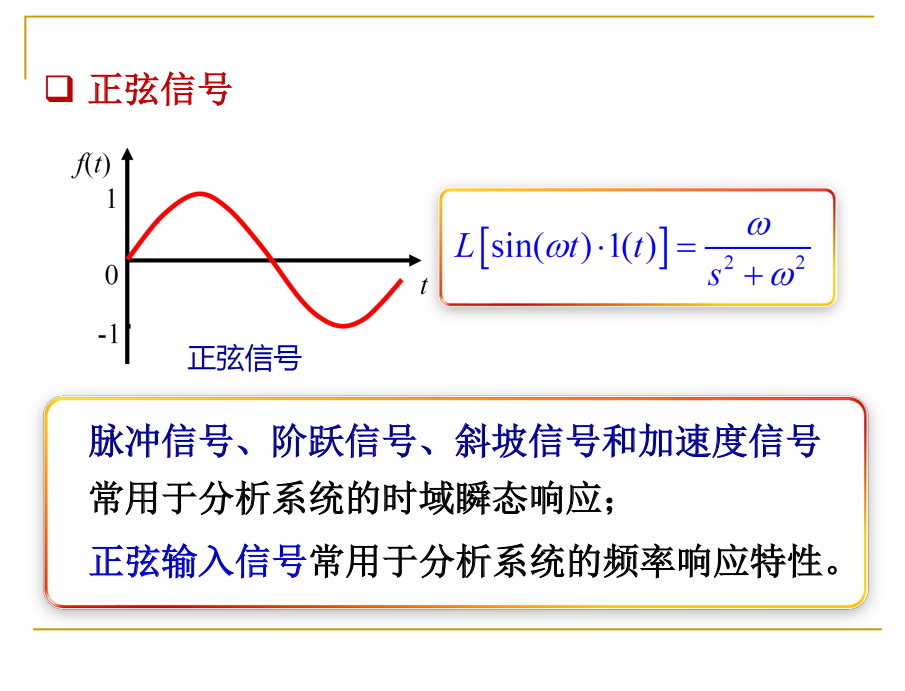
常见的输入信号:

1. 脉冲信号 $1$
2. 阶跃信号 $1/s$
3. 斜坡信号 $1/s^2$
4. 加速度信号 $1/s^3$
5. 正弦输入信号 $w/(s^2 + w^2)$

常见系统:

1. 一阶系统 $G(s) = 1/(Ts + 1)$
2. 二阶系统 $G(s) = (w_n^2)/(s^2 + 2\eta w_n s + w_n^2)$

瞬态响应和瞬态性能指标

时域分析中, 可分为瞬态过程和稳态过程来研究.

• 瞬态响应: 在输入状态下, 从初始态到稳定态的过程. 反映稳定性和快速性
• 稳态响应: t趋于无穷时, 系统输出的表现. 反映准确性.

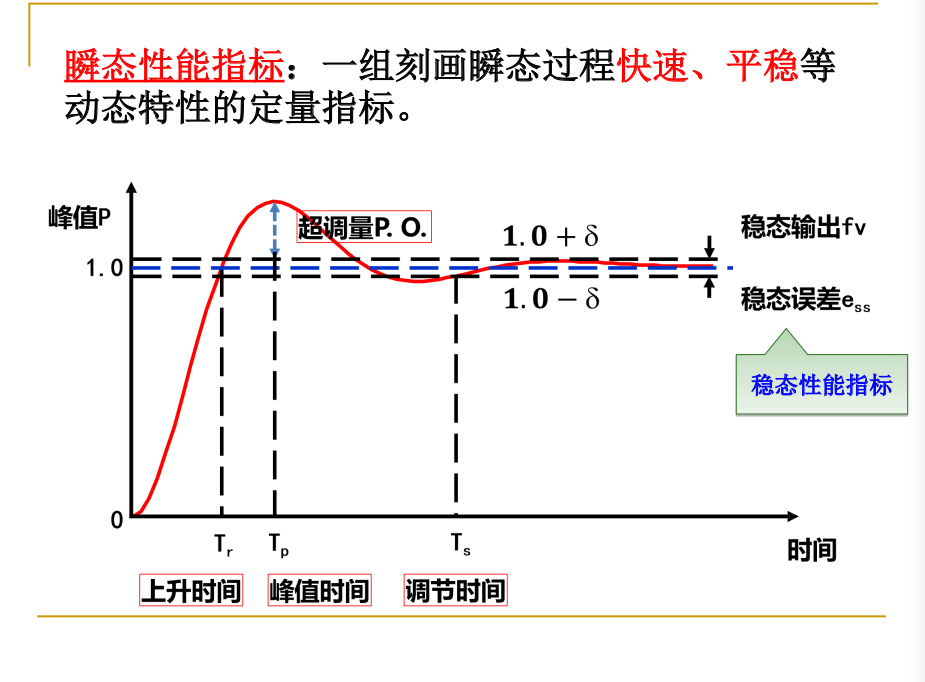
性能指标:

上升时间 Ries Time:
从零开始, 首次到达稳态值的时间 (有超调的系统 / 欠阻尼); 或从稳态值10%到90%的过程 (无超调的系统 / 过阻尼)

峰值时间 Peak Time:
从零开始, 到达首个峰值的时间

反映了系统的敏捷性

调节时间 Settling Time:
到达, 并始终保持在允许误差范围内的最短时间

标志过渡过程的结束, 衡量了系统响应的快速性

超调量 Percent Overshoot P.O. :
响应曲线最大峰值与稳态值1的差, 用百分比表示.

反映了系统的平稳性

震荡次数 Oscillation Number:
在调节时间内, 曲线振荡的次数 (看极值的数量?)

一阶系统时域响应性能分析

典型例子是RC低通滤波器 (这是个啥啊?)

• 中间只有一个一阶导元件作为一阶元件. 其参数称为时间参数, 为一阶系统唯一的性能参数
• 闭环时, 表现为一阶系统.

对于各种输入的响应曲线:

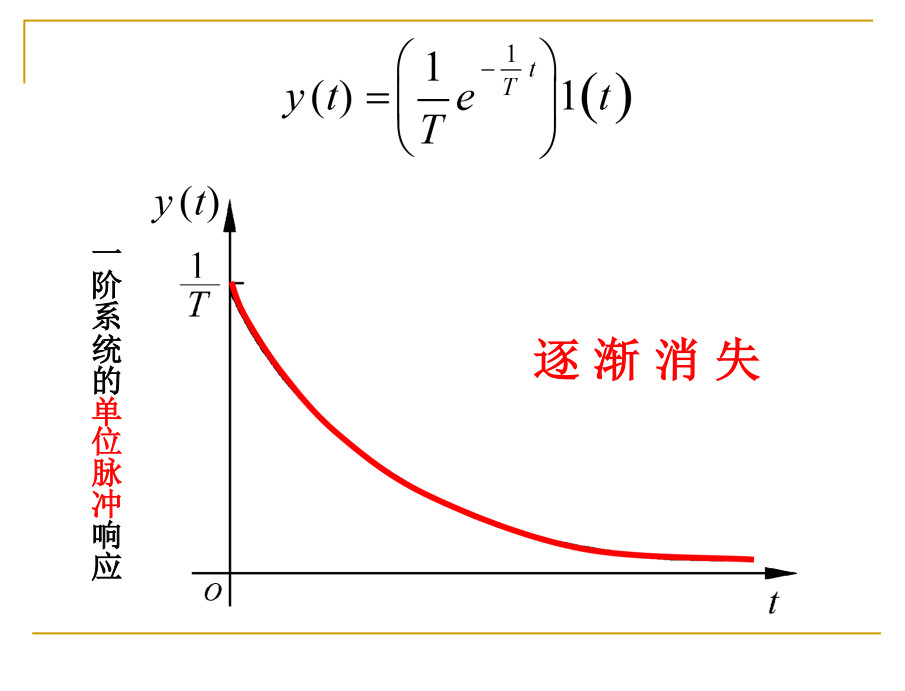
脉冲响应:

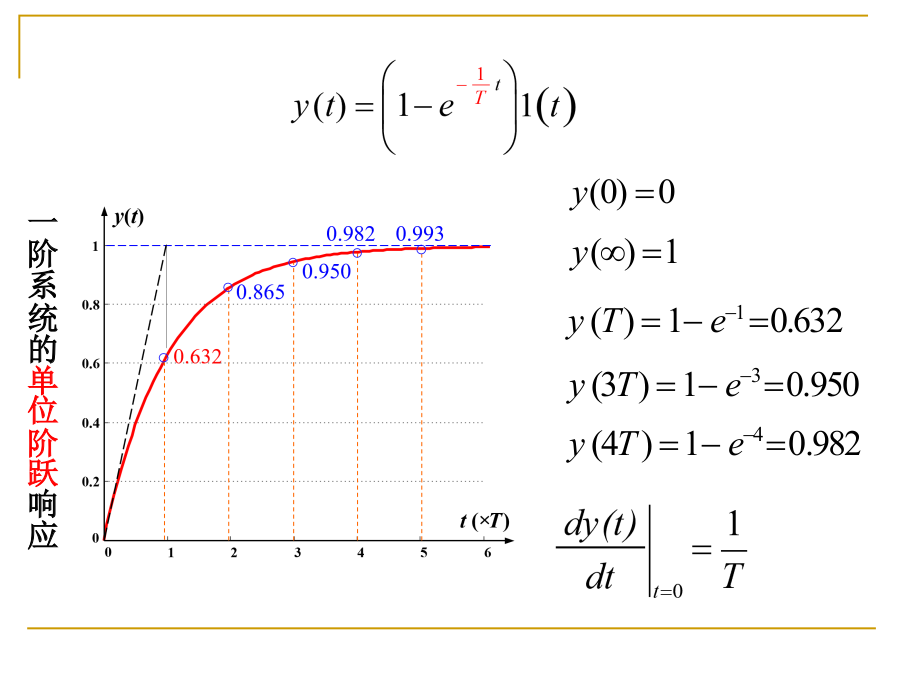
阶跃响应:

斜坡响应:

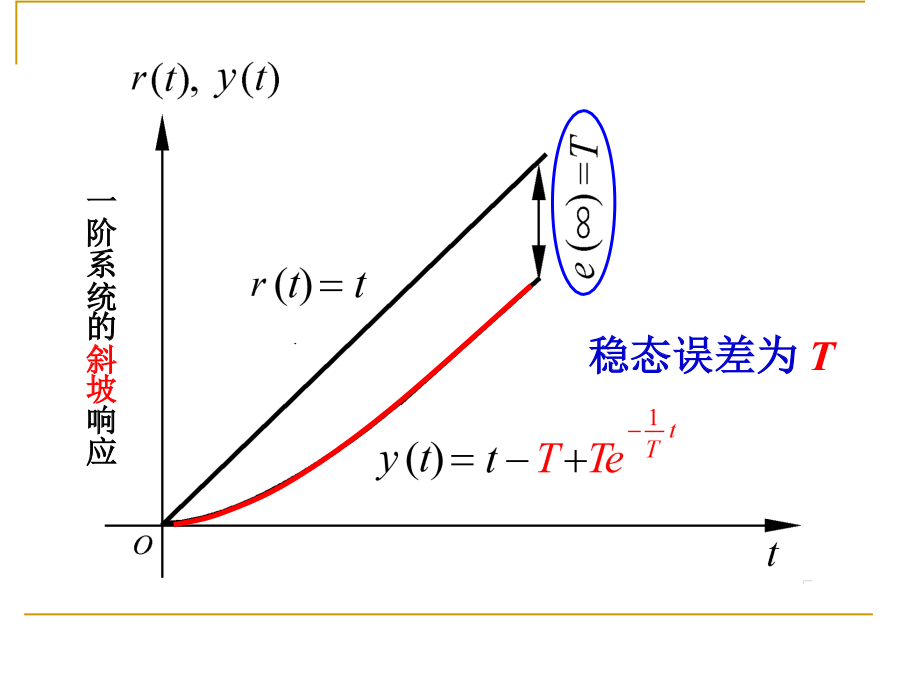
加速度响应: 任务复杂的时候, 有更恶劣的性能(无限偏差)

$$y(t) = \frac{1}{2} t^2 - Tt + T^2(1-e ^{-t/T}) = \frac{1}{2} t^2 - T(t - T(1-e ^{-t/T}))$$

1. 选择元器件, 减小时间常数
2. 引入反馈, 减小时间常数 (闭环传递函数再反馈一次. 反馈有功率损失的副作用)

二阶系统时域响应性能分析

二阶系统 $G(s) = (w_n^2)/(s^2 + 2\eta w_n s + w_n^2)$
开环传递函数为 $(w_n^2)/s(s + 2\eta w_n)$

上面为标准形式. 一般形式可加一个放大器.

其中两个参数分别称为 阻尼系数和系统固有频率(类似震荡频率)

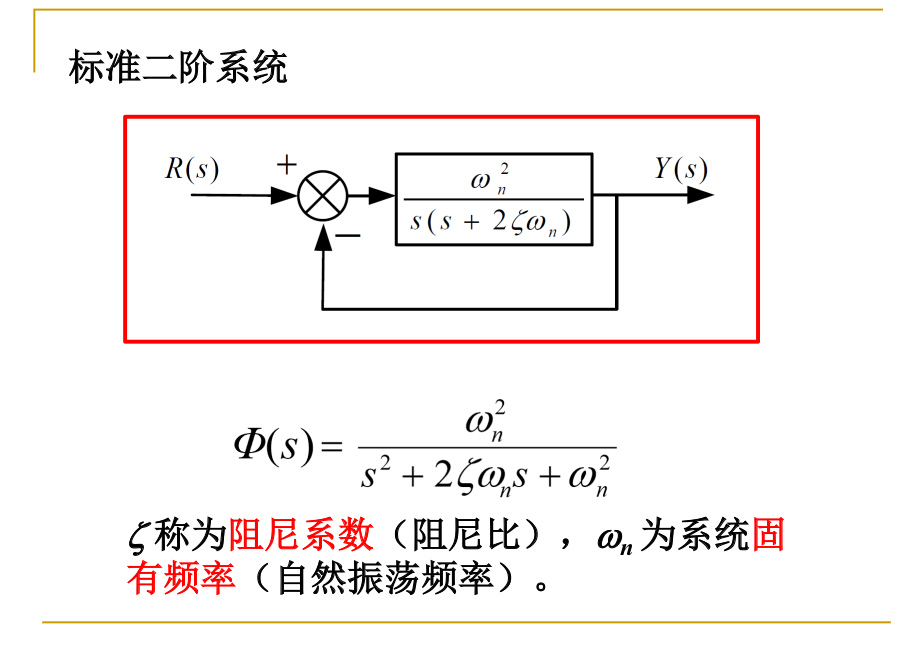
我们考虑阻尼系数.

当阻尼系数处于 $(0, 1)$, 式子是最复杂的.

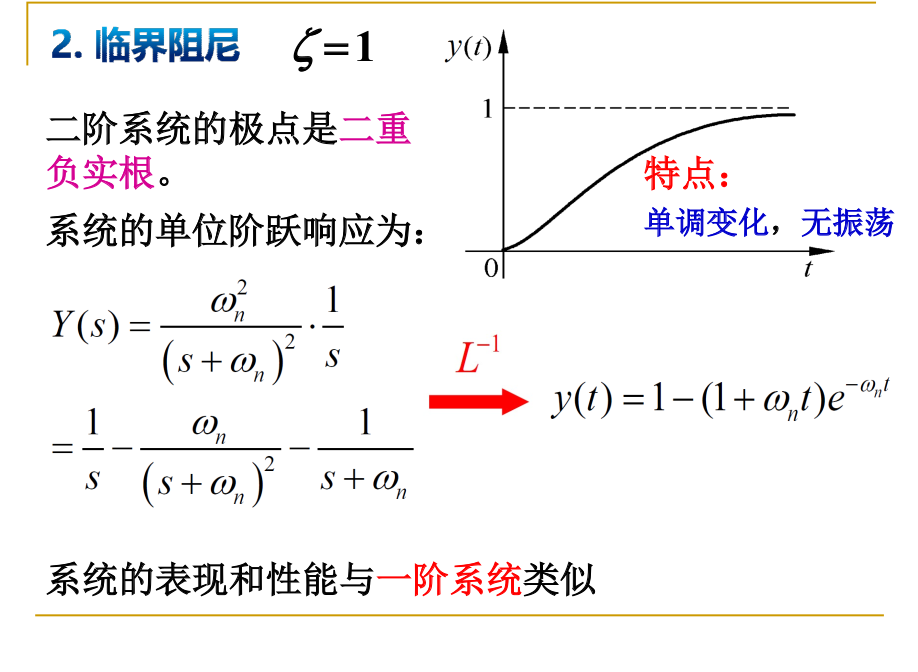
当阻尼系数为1时, 恰到好处. 既不会超调, 上升的也较快.

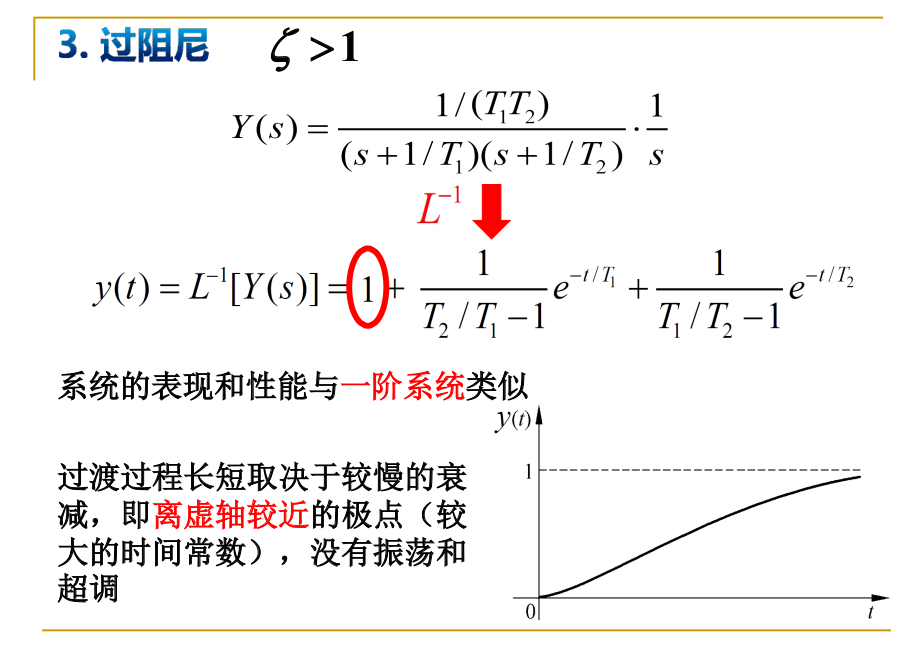
当阻尼系数大于1时, 同样不会超调, 但是上升更慢

性能与一阶系统类似. 采用和一阶系统类似的$T$参数
过渡过程取决于较慢的衰减过程, 即离虚轴较近的极点 ( 较大的时间常数)

过渡时间的长短取决于较靠近虚轴的极点. 所以临界阻尼的收敛速度是最快的(较近的极点离得最远); 而0阻尼则不收敛(极点在虚轴上)
过阻尼和临界阻尼的性质都类似一阶系统.

当阻尼系数为0时, 持续震荡.

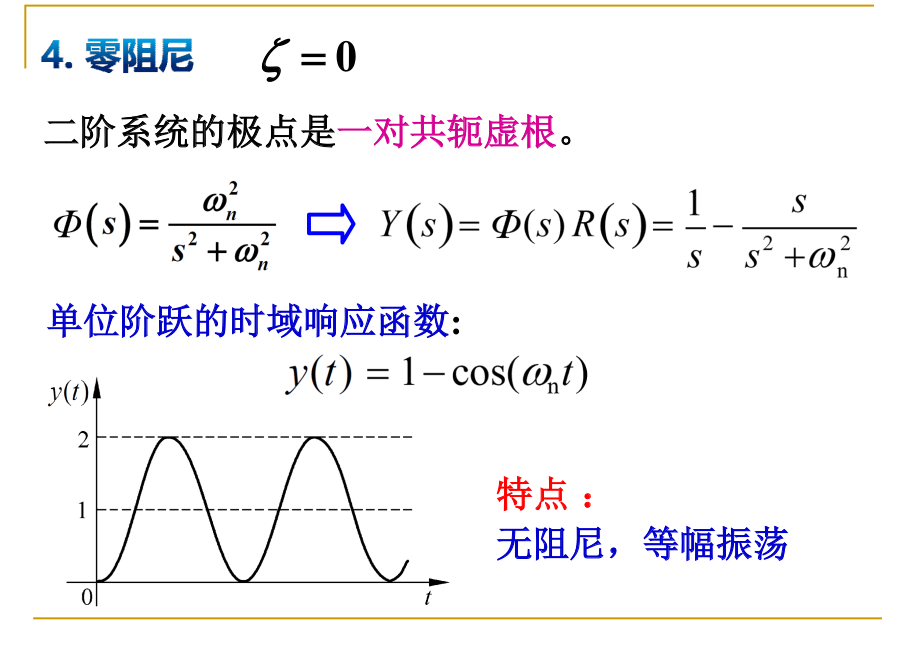
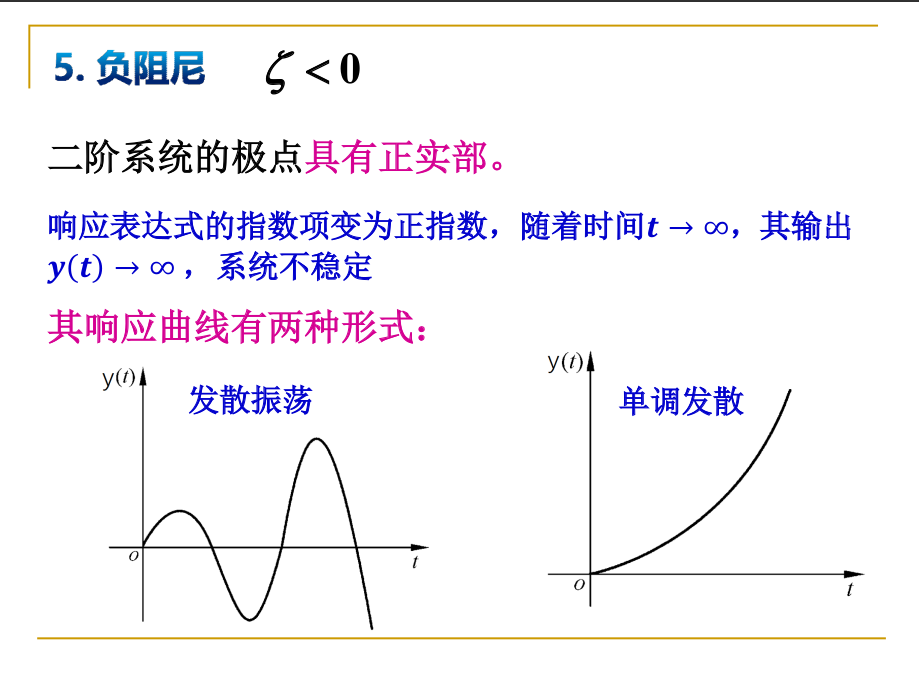
当阻尼系数小于0时, 发散

欠阻尼系统性能指标计算

对于阶跃函数:

$$\beta = \arccos \eta = \arctan \frac{\sqrt{1 - \eta^2}}{\eta}$$

稳态误差为零.

上升时间为

$$t_r = \frac{\pi - \beta}{ w_d} =\frac{\pi - \beta}{ w_n\sqrt{1 - \eta ^2}}$$

峰值时间为

$$t_p = \frac{\pi}{w_d} = \frac{\pi}{\sqrt{1 - \eta ^2}}$$

超调量为

$$P.O. = \exp\frac{- \pi \eta }{\sqrt{1 - \eta ^2}} \cdot 100\%$$

调节时间为

$$t_s = \frac{-\ln \delta - \ln \sqrt{1 - \eta ^2}}{\eta w_n} \approx (-\ln \delta) T$$

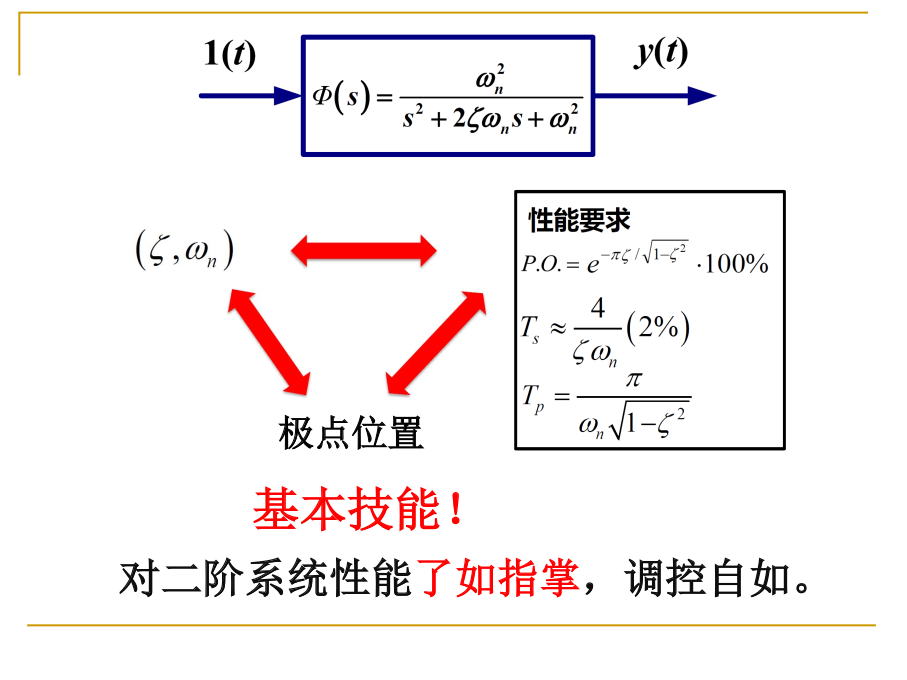
极点与系统的各种指标的关系:

等阻尼$\eta$线($\beta, P.O.$线)
此线上, 极点的实虚部比值相等, $\beta, P.O.$的值不变.

等$w_n$线
此线上, 极点$w_n(-\eta +- j \sqrt{1 - \eta^2})$的模长相等, $w_n$的值不变.

等$t_s$线
对于单位过渡时间 $T_s = \frac{1}{\eta w_n}$, 它的值就是极点实部的值. 因此过渡时间只与实部有关

等$t_p$线
对于峰值时间 $T_p = \frac{\pi}{w_n \sqrt{1 - \eta^2}}$, 它的分母就是极点虚部的系数. 因此峰值时间只与虚部有关

好漂亮的性质啊. 这是巧合吗?

Example:

1. 已知极点, 求各种指标, 如调节时间, 超调量, 峰值时间: 先解出阻尼系数和系统自然频率
2. 已知阶跃响应时域图像, 求传递函数: 先根据稳态输出得到待定系数式, 再根据各种指标, 如超调量, 确定阻尼系数和系统自然频率
3. 参数设计, 即给出各种性质的要求, 确定满足要求的增益系数K和相关参数: 图像性质.

高阶系统时域响应性能分析

将高阶系统的式子化为若干一阶惯性环节和二阶振荡环节的叠加.

对于一个高阶系统, 其转移函数为

$$G(s) = \frac{Y(s)}{R(s)} = K\frac{s^m + b_1 s^{m-1} + ... + b_{m-1} s + b_m} {s^n + a_1 s^{n-1} + ... + a_{n-1} s + a_n}$$

可将分母化作若干一阶式和二阶式连乘的结果 (实根和复根)

$$H^(n)(s) = \prod_{q}^{j = 1} (s + p_j)\prod_{r}^{k = 1} (s^2 +\eta_k w_k s + w_k)$$

其中 $m \leq n, q + 2r = m$

• 高阶系统的瞬态响应由若干一阶环节与二阶环节叠加组成
• 当所有闭环极点均具有负实部时, 系统稳定; 否则不断振荡

---

额外闭环零点 / 极点对性能的影响

高阶时, 情况更加复杂.
我们考虑在二阶系统上添加一个额外环节:

1. 接上一个微分环节 $\frac{s+z}{z}$. 此时原有输出被微分环节调理, 波动增强(类似减小阻尼系数). 零点越靠近虚轴, 效应越明显.
2. 接上一个积分环节 $\frac{s+z}{z}$. 此时原有输出被积分环节调理, 波动减弱(类似增大阻尼系数). 极点越靠近虚轴, 效应越明显. 所以, 当极点很远离虚轴时, 可以将其忽略. (根据分解式, 此时该极点的影响指数衰减, 且速度非常快)

高阶系统简化

1. 忽略非主导极点: 当远处极点的距离超过近处极点10倍时, 可以忽略远处极点, 将近处极点作为主导极点 . (近处极点附近需要没有零点) (注意要保证系统的静态增益不变)
2. 偶极子相消: 若具有负实部的零点和极点在数值上相近(互相 之间的距离小于本身距离的十分之一), 则可以将零点和极点一起消掉.

于是, 可以将一些高阶系统近似为二阶系统, 然后按照已有的方法进行分析.

系统的稳态性能分析

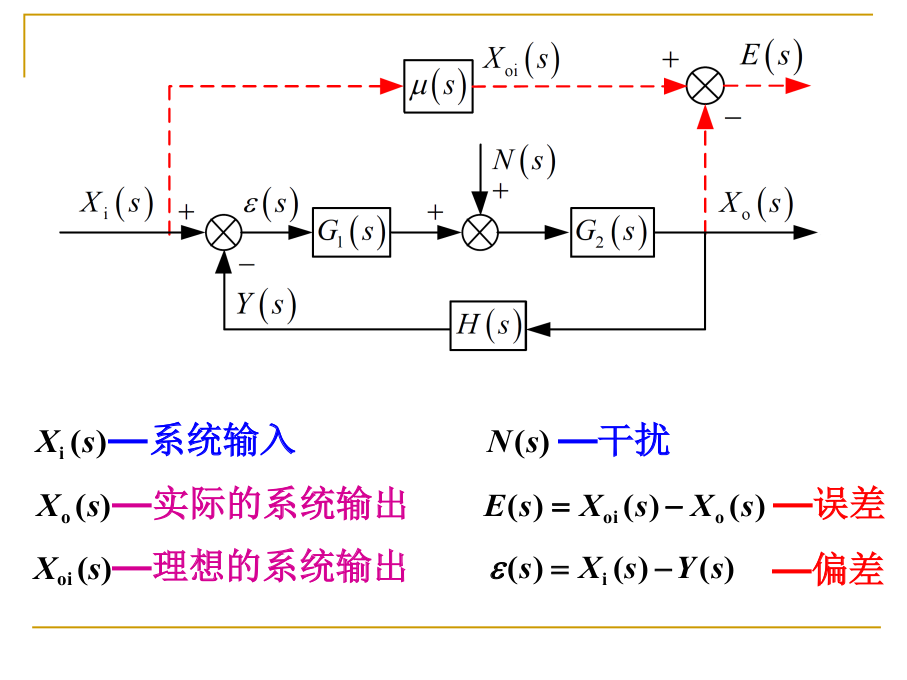
误差$e(t)$ :系统 理想输出和实际输出的差
偏差$\epsilon(t)$ :系统输入信号和反馈信号的差

此处, 考虑了理想输入与实际输入信号的差别, 同时考虑了实际输出和反馈信号的差别.
误差是理想化的偏差, 偏差是实际仪器能测得的误差. (某种程度上)

输入到输出的传递关系(不存在干扰的情况):

$$\frac{X_o(s)}{X_i(s)} = \frac{G_1(s)G_2(s)}{1 + G_1(s)G_2(s)H(s)}$$

当 $G_1(s)G_2(s)H(s) >> 1$时, 将1忽略, 有

$$\frac{X_o(s)}{X_i(s)} \approx \frac{1}{H(s)}$$

于是, 理想化的输入输出关系为

$$X_{oi}(s) = \mu (s) X_o(s) = \frac{1}{H(s)} X_i(s)$$

自动控制系统的唯一目标就是(令 $H(s)$ 为常数)

$$X_{oi}(t) = \frac{1}{H} x_i(t)$$

即, 除了一个系数增益, 将所有期望的变化过程都直接进行传递

公式推导: 当反馈通道不存在干扰时
当令 $\mu(s) = \frac{1}{H(s)}$

$$E(s) = \frac{\epsilon (s)}{H(s)}$$

• 对于实际的系统, $H(s)$往往是一个常数. 于是求出了稳态偏差也就求出了稳态误差
• 对于单位反馈系统, 偏差与误差相同.

输入引起的稳态误差

一. 偏差传递函数与稳态误差

当不存在干扰时, 可以直接考虑 $G(s), H(s)$

偏差传递函数为

$$\frac{\\epsilon (s)}{X_i(s)} = \frac{1}{1 + G(s)H(s)}$$

当系统稳定时, 求稳态偏差为:

$$\epsilon _{ss} = \lim_{t \rightarrow \infty} \epsilon(t) = \lim_{s \rightarrow 0} s\epsilon(s) = \lim_{s \rightarrow 0} s\frac{1}{1 + G(s)H(s)} X_i(s)$$

稳态误差为

$$e_{ss} = \lim_{s \rightarrow 0} E(s) = \lim_{s \rightarrow 0} [\epsilon(s) / H(s)] = \epsilon _{ss} / H(0)$$

稳态误差取决于系统的结构参数和输入信号的性质

二. 系统的型次

根据前面的分析, 我们只需要求解一个传递函数和一些极限, 就可以得到系统的稳态误差 / 稳态偏差

我们考虑系统的开环传递函数(对于反馈信号)

$$G(s)H(s) = \frac{K(a_1s + 1)(a_2s + 1) ...}{s ^{\lambda} (T_1s + 1)(T_2s + 1) ...}$$

当求极限时, 括号中的内容都变为常数, 重要的只有外面的$\lambda$:
我们根据lambda的值, 称系统为 0型/ 1型 / 2型系统.

根据

$$\lim_{s \rightarrow 0} s\frac{1}{1 + G(s)H(s)} X_i(s)$$

我们可以讨论不同信号, 不同型次系统的稳态偏差:

定义静态位置误差系数 (若函数连续? 或许可以通过laplace变化的性质来保证连续性):

$$K_p = \lim_{s \rightarrow 0} G(s) H(s) = G(0)H(0)$$

则

对于单位阶跃响应, 稳态误差为

$$\epsilon_{ss} = \frac{1}{1 + K_p}$$

• 0型系统, $K_p = K$, $\epsilon_{ss} = \frac{1}{1 + K}$
• 1型及更高型次的系统: $K_p = \infty$, $\epsilon_{ss} = 0$

定义静态速度误差系数:

$$K_v = \lim_{s \rightarrow 0} s G(s) H(s)$$

则

对于单位斜坡响应, 稳态误差为

$$\epsilon_{ss} = \frac{1}{K_v}$$

• 0型系统, $K_v = 0$, $\epsilon_{ss} = \infty$
• 1型系统: $K_v = K$, $\epsilon_{ss} = 1/K$
• 2型系统: $K_v = \infty$, $\epsilon_{ss} = 0$

定义静态加速度误差系数:

$$K_a = \lim_{s \rightarrow 0} s^2 G(s) H(s)$$

则

对于单位加速度响应, 稳态误差为

$$\epsilon_{ss} = \frac{1}{K_a}$$

• 0型系统, $K_v = 0$, $\epsilon_{ss} = \infty$
• 1型系统: $K_v = 0$, $\epsilon_{ss} = \infty$
• 2型系统: $K_v = K$, $\epsilon_{ss} = 1/K$

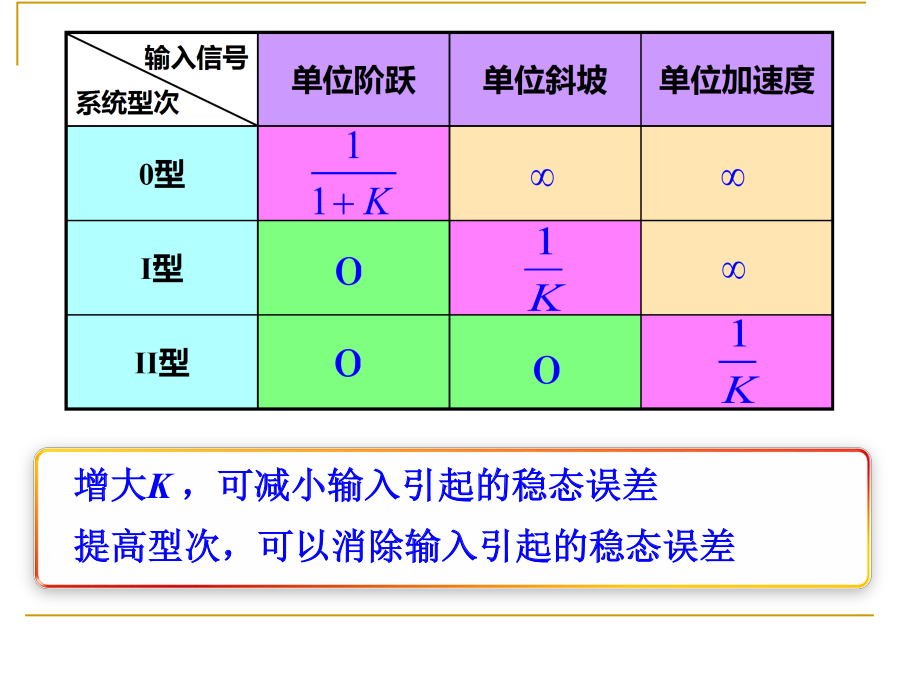
因此, 只要将系统的开环函数化为上述形式, 然后求解系统的型次及相关极限即可.

干扰引起的稳态误差

由于

$$\epsilon (s) + \epsilon(s) G_1(s)G_2(s)H(s) + N(s)G_2(s)H(s) = X_i(s)$$

所以, 当我们不考虑输入时, 可以得到干扰引起的偏差的传递函数为

$$\frac{\epsilon(s)}{N(s)} = \frac{-G_2(s)H(s)}{1 + G_1(s) G_2(s) H(s)}$$

类似求偏导. 无关变量连同其系数一起被忽略. (线性系统)

求极限, 便可以得到相应的稳态误差和稳态偏差.

也可以直接求出由干扰引起的输出, 然后根据定义直接求的干扰引起的误差 (不经过偏差的求解. )

---

总结:

1. 系统误差包括输入引起的误差和干扰引起的误差
2. 求解系统稳态误差应当首先判断系统的稳定性
3. 当两个量同时作用时, 求解线性系统的偏差, 可以利用叠加原理

Example:

• 误差前增益 $K_1$越大, 稳态误差越小.
• 即, 可以通过增大前向通道干扰点前的 放大倍数来减小干扰带来的稳态误差.
• 在干扰点前加积分器 $1 + \frac{K_3}{s}$, 总式子为$K_1(1 + \frac{K_3}{s})$, 可以消除干扰带来的稳态误差影响

总结: 要使得干扰引起的稳态误差尽量小, 干扰输入点前的增益应当尽量大, 甚至带积分环节.

• 系统反馈通道的测量干扰带来的误差无法消除

减小稳态误差的途径

1. 提高反馈通道的精度, 避免在反馈通道引入干扰
2. 系统稳定的前提下, 对于输入引起的误差, 可以增大系统的开环放大倍数(首选, 有差工作状态), 或者提示系统的型次(有显著副作用)
3. 对于干扰引起的误差, 可以增大干扰点前的放大倍数(减小误差), 或者在干扰点前加积分器(消除误差)

MATLAB 在时域分析中的应用

求单位阶跃响应:

绘制响应曲线
step(sys)或step(sys, t)
step(num, den)或step(num, den, t)

求解响应数据
[y, t] = step(sys)或y = step(sys, t)
[y, t] = step(num, den)或step(num, den, t)

求单位脉冲响应:

绘制响应曲线
impulse(sys)或impulse(sys, t)

求解响应数据
[y, t] = impulse(sys)或y = impulse(sys, t)

求任意输入下系统的输出响应:

绘制响应曲线
lsim(sys, u, t)
u是给定输入构成的列向量, 即t时刻的输入值

求解响应数据
[y, t] = lsim(sys, u)或y = lsim(sys, u)

由于没有斜坡响应命令, 我们可以用s除$G(s)$, 再求它的阶跃响应

---

总结

一阶系统的瞬态响应:

• 脉冲, 阶跃响应为对数型曲线, 稳态误差为0; 斜坡响应稳态误差为常数
• 稳定性, 快速性与准确性均与系统固有特性有关 (即与参数T有关); 仅准确性与输入信号的形式有关 (?)

二阶系统的瞬态响应:
主要分析欠阻尼状态以及单位脉冲响应

时域分析指标:
上升时间
峰值时间
超调量
调节时间

极点位置与瞬态响应特性的关系

高阶系统的性质及其简化方法

• 忽略非主导零极点
• 偶极子相消

系统稳态性能分析

• 误差与偏差
• 静态位置误差系数, 静态速度误差系数, 静态加速度误差系数