LearnLog

学习Automata PPT的记录. 相关笔记会另开博客记录. 也可能不会开.

Pumping Lemma for CFL

  • for every context-free language L
  • There is an integer n, such that
  • for every string z∈Lz \in L of length ≥n\geq n
  • There exists z=uvwxyz = uvwxy such that:
    1. ∣vwx∣≤n|vwx| \leq n
    2. ∣vx∣>0|vx| > 0
    3. For all i≥0i \geq 0, uviwxiy∈Luv^iwx^iy \in L

即: 对于足够长的字符串, 满足Pumping Lemma

证明:

Lemma1: 对于包含m个变量的, CNF语法, n=2mn = 2^m,
则对于len≥nlen \geq n的字符串z, 他的生成树足够高.

换言之, A parse tree with yield z must have a path of length m+2m + 2 or more.

于是, 由于生成路径足够长, 路径上一定会有重复的变量. 令其为A.

则

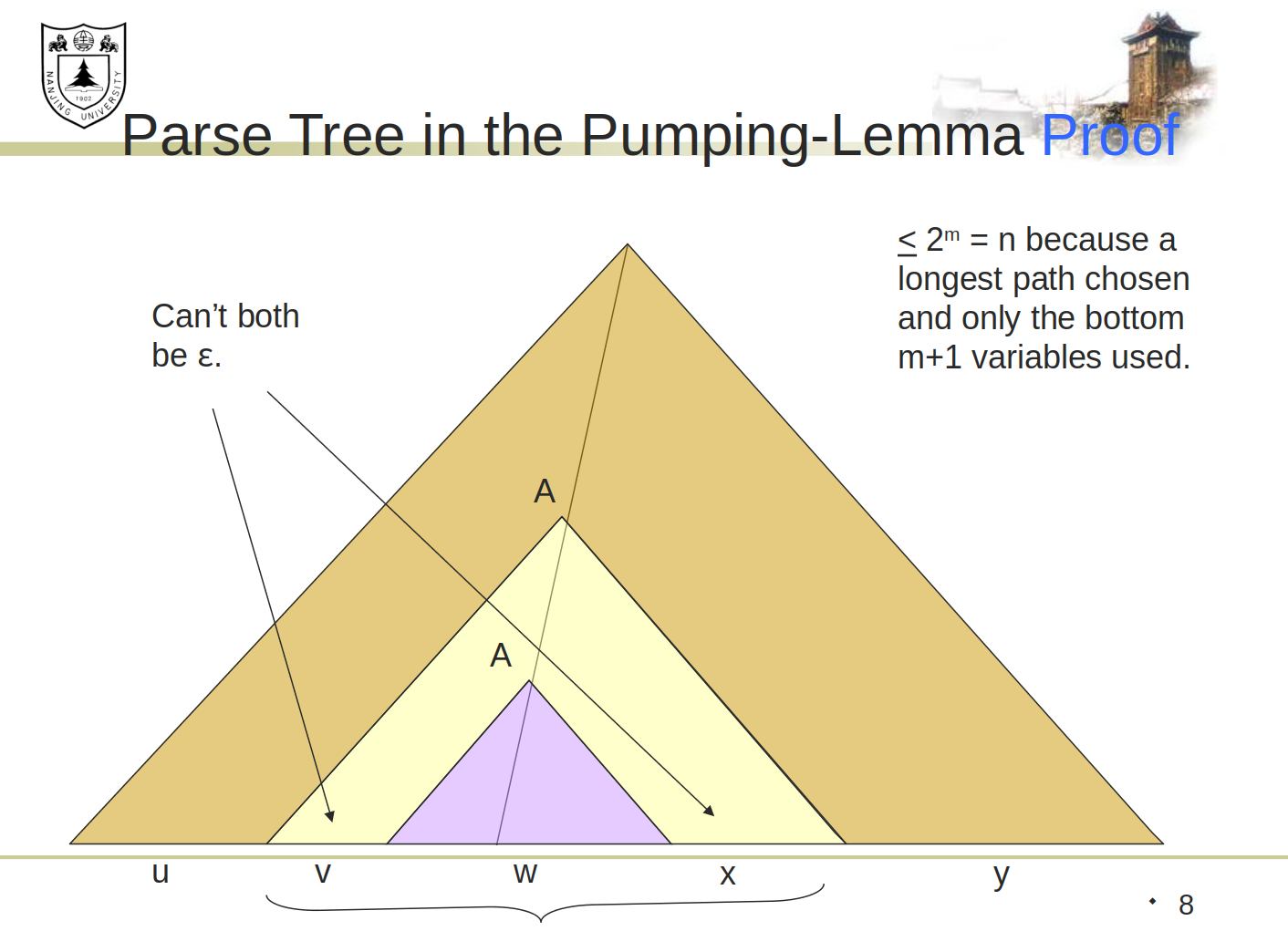
相当于, 我们构造性地证明了 production A -> vAx的正确性. 因此可以不停地扩展之.

Example:
我们可以证明,

  • {0i10i∣i≥1}\{0^i10^i | i \geq 1\} 是CFL
  • 而{0i10i10i∣i≥1}\{0^i10^i10^i | i \geq 1\} 不是CFL. 同理, 更多pair的语言也不是CFL.
  • (CFL只能描述"头尾性质"的语言)

证明: 假设{0i10i10i∣i≥1}\{0^i10^i10^i | i \geq 1\} 是CFL. 那么满足Pumping Lemma.
对于z=0n10n10nz = 0^n10^n10^n分类讨论, 考虑它划分为z=uvwxyz = uvwxy的方式. 并发现每种case 都是不合法的.

证毕.

Properties of CFL

  • Decision Properties
  • Closure Properties

Decision Properties

  • 很多RE相关的问题, 都不能在CFL上进行判断
  • 如, 两个CFL是一样的吗?
  • 两个CFL是disjoint的吗?
  • 通过Turing machines 的理论, 来证明不存在这样的算法.

判断CFL是否是empty的:
即, 判断起始符号是否为useless variables.

判断w是否在 L(G)L(G)当中:
通过算法 CYK来完成, 采用DP算法, O(n3),n=∣w∣O(n^3), n = |w|

  • 对于w=a1...anw = a_1...a_n, 构建变量 Xij={A∣A⇒∗ai...aj}X_{ij} = \{A| A \Rightarrow ^*a_i...a_j\}
  • 从长度开始DP, 从1到n. (DP过程根据CNF的production显然. )

判断CFL是否是infinitness的:
即, 判断是否有长度超过n的字符串. 如果有, 根据Pumping Lemma, 该语言是无限的.

Closure Properties

CFL’s are closed under

  • union, concatenation, Kleene closure
  • reversal, homomorphisms, inverse homomorphisms

But not under

  • intersection or difference

证明:

  • 考虑两个语言G, H, 并令他们的变量各不相同.

union:

  • 构造新的CFG. 仅仅令 S=S1∣S2S = S_1 | S_2即可.

concatenation:

  • 构造新的CFG. 仅仅令 S=S1S2S = S_1S_2即可.

Kleene closure

  • 构造新的CFG. 仅仅令 S=ϵ∣S1SS = \epsilon|S_1S即可.

reversal

  • 翻转production. 在CNF下很容易, 非CNF也不难.

homomorphisms and inverse homomorphisms

  • 相应地构造相关的CFG 即可.

对于intersection的反例:

  • L2={0n1n2i∣n,i≥1}L_2=\{0^n1^n2^i|n, i \geq 1\}和L3={0i1n2n∣n,i≥1}L_3=\{0^i1^n2^n|n, i \geq 1\}都是CFL
  • 但是L1=L2∩L3={0n1n2n∣n≥1}L_1= L_2 \cap L_3=\{0^n1^n2^n|n \geq 1\}不是CFL. (可通过Pumping Lemma证明)

对于difference的证明:
我们有

L∩M=L−(L−M)L \cap M = L - (L - M)

于是,

  • “任何在difference 下封闭的语言都在intersection下封闭”
  • 因此, “任何不在intersection下封闭的语言都不在difference 下封闭”

对于intersection的更多性质:

  • CFL与CFL 的intersection不一定是CFL. (反例在上面已经给出)
  • CFL与RL 的intersection 一定是CFL. (证明: 注意到PDA和DFA的combination还是PDA)

关于homomorphisms 的更多讨论

  • DFA之间的转换, gramma dont help us
  • 但是, 我们可以通过PDA之间的转换, 来证明homomorphisms的正确性. (构造 + 递归)
backtop