LearnLog

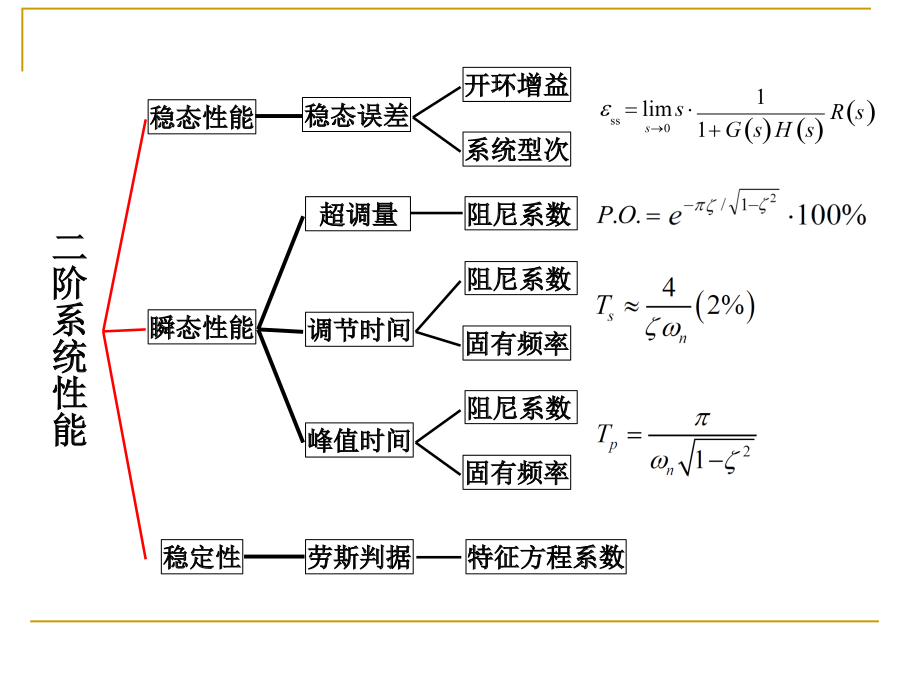
学习控制理论课程PPT的记录. 相关笔记会另开博客记录. 也可能不会开.

稳定性的基本概念

平衡状态: 若没有受到任何扰动或输入信号的激励, 输出量将保持在某个状态.

dxdt=0\frac{dx}{dt} = 0

稳定性: 处在平衡态的系统, 在扰动作用后, 当扰动消失时, 扰动的后效会随着时间消失. 此时称系统是稳定的.

  • 处于平衡态时, 具有一定的抗干扰能力.
  • 不仅要求导数为0, 而且要求二阶导大于0.

更加严格的定义:

  • 有界输入有界输出 (BIBO): 有界输入的激励下, 系统只会产生有界的输出
  • 扰动消失稳定, Lyapunov稳定性
  • 稳定性是系统的固有属性

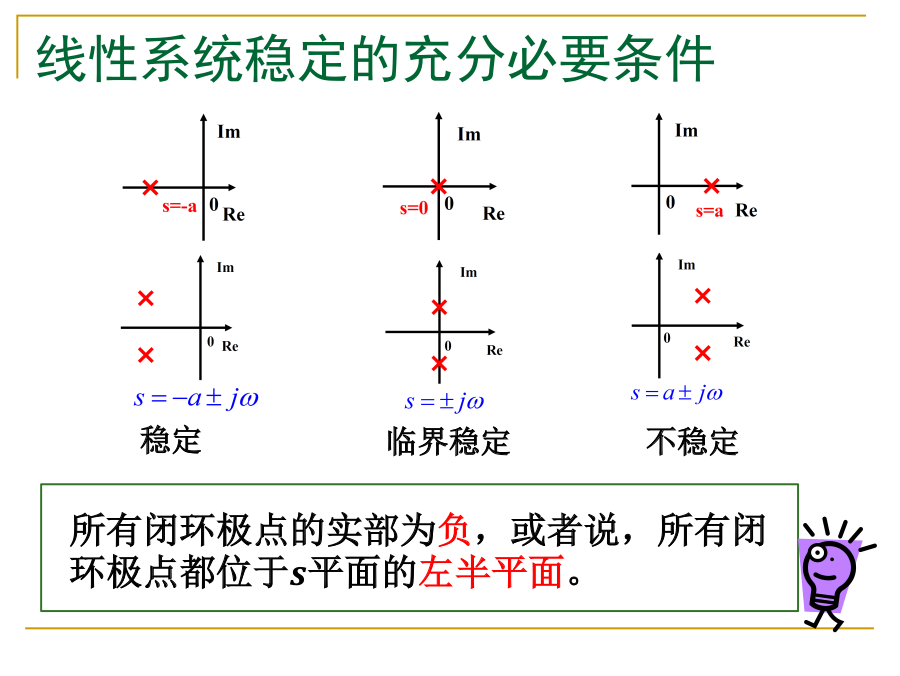
线性系统稳定的充分必要条件

对于单位脉冲响应:

根据逆拉普拉斯变换可以直接得到.

由于: 输出是有界输入与单位脉冲响应的卷积(组合)
因此, 我们只需要考虑 "闭环传递函数的脉冲响应是否有界"即可.

  • 若所有极点的实部为负: 有界(稳定)
  • 若有一个非负(原点或虚轴上有单重极点), 一般有界(稳定), 但对于特定的输入产生共振, 导致无界(不稳定)
  • 若多个非负, 则一定不稳定

所以: 线性系统稳定的充要条件为 (两种等价表述)

  • 所有闭环极点的实部为负
  • 或 所有闭环极点位于s平面的左半平面

判断是否稳定的最直接方法:
求出系统 闭环特征方程的根
(阿贝尔定理: 五次及更高次的代数方程没有一般的代数解法, 方程的根不能通过方程系数经过有限次四则运算和开方运算求得)

劳斯-赫尔维茨稳定性判据

即: 在不求出根的前提下, 判断稳定性

根据韦达定理:

an−1an=−(s1+s2+...+sn)\frac{a_{n-1}}{a_n} = -(s_1 + s_2 + ... + s_n)

an−2an=+(s1s2+s1s3+...+sn−1sn)\frac{a_{n-2}}{a_n} = +(s_1s_2 + s_1s_3 + ... + s_{n-1}s_n)

......

a1an=(−1)n(s1s2s3...sn)\frac{a_{1}}{a_n} = (-1)^n(s_1s_2s_3...s_n)

于是得到必要条件为

  1. 特征方程的各项系数不为0
  2. 特征方程的各项系数同号

由于 ana_n一般为正, 所以上面的条件简化为 ai>0a_i > 0

称为劳斯判据.

由于只是必要条件, 因此系数全正的方程, 系统是否稳定还需要进一步考察

充要条件: 劳斯-赫尔维茨稳定性判据

  1. 特征方程各项系数为正 ai>0a_i > 0
  2. 劳斯判定表中第一列所有项为正 (实部为正的特征根数等于劳斯判定表中第一列的系数符号改变的次数)

计算方法:

  1. 第一, 二行直接通过系数得到
  2. 前两行的四个数列为行列式, 除以左下角, 取负号.
  3. 不存在的补为0; 首列为0, 用无穷小正数代替0, 继续运算; 存在全零行, 系统不稳定

劳斯-赫尔维茨稳定性判据的应用

根据判据, 来设计稳定系统应当有的参数

  • 若要求相对稳定性 (特征值位于垂线左侧): 用 s−as - a替换 ss, 得到新的多项式

MATLAB在稳定性分析中的应用

可利用MATLAB求近似解.

总结

backtop