LearnLog

学习控制理论课程PPT的记录. 相关笔记会另开博客记录. 也可能不会开.

根轨迹的基本概念

考虑下面的二阶系统的性能

因此, 我们考虑一般的情况, “比例控制结构”, 并给出这个结构下, 参数变化对于系统性能的影响

  1. 给出特征方程的根, 根表示为包含参数的一般形式
  2. 考察参数K从零到无穷大时, 根的轨迹变化情况

约束条件: 考察某个极点是否会在轨迹上
在轨迹上的点必须满足

1+KG(s)H(s)=01 + KG(s) H(s) = 0

于是, 将方程展开得到

∣KG(s)H(s)∣=1|KG(s)H(s)| = 1

同时, "零点角度"减去"极点角度"为 −180-180度. 其中零点, 极点角度为零极点指向 ss的向量的角度. (此处零极点为开环零极点)

  • 相角条件决定了整条根轨迹, 即决定了哪些点是极点 (充要条件)
  • 幅值条件决定了极点 ss 的匹配增益值.

根轨迹绘制的基本方法

  1. 根轨迹的分支数: N阶系统有N个闭环极点. 根轨迹的分支数等于系统阶数, 也等于开环极点的个数
  2. 根轨迹的对称性: 关于实轴对称 (要么都是实根, 要么都是共轭复根)
  3. 根轨迹的起点: 起始于开环极点 (展开, 令 K趋于0即可得到)
  4. 根轨迹的终点: 终止于开环零点
  5. 实轴上的根轨迹段: 考察其右侧的开环零极点个数之和的奇偶性, 来判断相角和 (这是由于: 共轭开环零极点诱导的相角成对出现且和为360; 左侧实开环零极点相角为0. 因此只考虑右侧实零极点即可)
  6. 根轨迹的分离 / 会合点: 与特征方程的重根对应. 由于 K=−Q(s)P(s)K = -\frac{Q(s)}{P(s)}, 因此可以得到: 匹配增益值函数分支在极点 ss的实定义域内单调增减, 且在分离点处取最大值, 在会合点处取最小值 (根据图像)

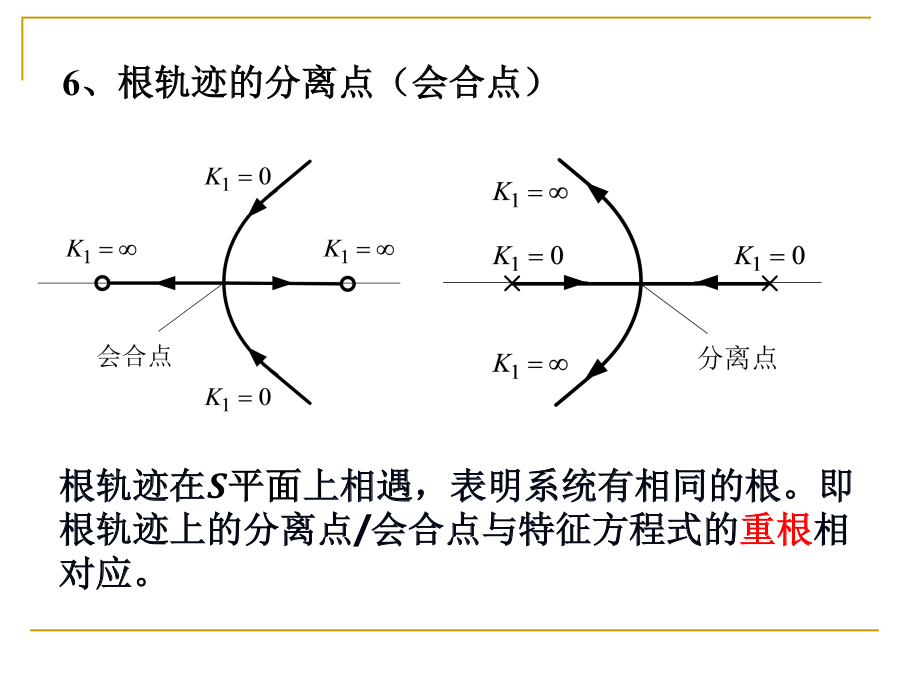
因此, 我们可根据必要条件

dKds=−P(s)Q′(s)−P′(s)Q(s)P2(s)=0\frac{dK}{ds} = - \frac{P(s)Q'(s)-P'(s)Q(s)}{P^2(s)} = 0

以及 K≥0K\geq 0 且为实数的约束条件, 即可得到真正的分离点和会合点 (求出对应的 ss 根)

  1. 根轨迹的渐近线
    n−mn - m条根轨迹分支, 沿着一组渐近线趋于无穷远处. 它们共享一个渐近中心 (与实轴相交)

σA=∑ni=1(−pi)−summj=1(−zi)n−m\sigma_A = \frac{\sum_{n}^{i = 1} (-p_i) - sum_{m}^{j = 1} (-z_i)}{n - m}

夹角为

ϕA=(2k+1)180n−m,k=0,1,...,n−m−1\phi_A = \frac{(2 k + 1) 180}{n - m}, k = 0, 1, ..., n - m - 1

渐近线平分360度. (180; 90, 270; 60, 180, 300; 45, 135, 225, 315; …)

  1. 根轨迹与虚轴的交点
    A. 利用特征方程求解: 即, 待定系数法, 令 s=jws = jw并求解特征方程, 得到对应的 ww 和 KK
    B. 劳斯判据求解: 确定K在稳定性改变的临界点, 在带入特征方程求得 jwjw的值

总结: 给定特征方程, 绘制轨迹图

第一步: 确定起始和终止点, 即求解开环函数的零极点 (零点不存在时, 看作无穷)

第二步: 确定实轴上的根轨迹段

第三步: 确定分离点或会合点. 求解导数为零的根, 并代回特征方程, 舍去 K<0K < 0的解.

第四步: 确定渐近线. 根据公式确定倾角和渐进中心

第五步: 确定轨迹与虚轴交点. 根据特征方程待定系数法求得.

第六步: 用平滑曲线, 将分离/会合点向渐近线靠近, 并补全实轴部分.

  1. 根轨迹的入射角和出射角
  • 当开环零极点为实数时, 根轨迹沿实轴发展, 不考虑入射角 / 出射角
  • 当开环零极点为复数时, 将根轨迹离开复极点的角度称为出射角, 将趋于复极点的角度称为入射角

当根轨迹点趋于开环零极点时, 依然满足相角和的性质, 同时轨迹点 ss与开环零极点的角度, 等价于趋近的点 prp_r与其他零极点的角度. 于是根据这个可求解出入射角和出射角

小结: 对于典型控制结构"比例控制", 我们可以绘制其根轨迹图, 从而刻画调节 KK时, 极点位置和系统性能变化的全貌.

基于根轨迹的控制系统分析

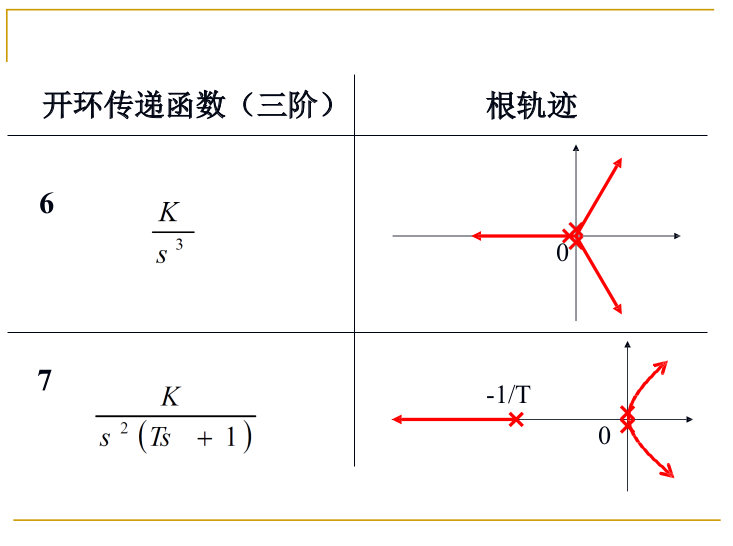
典型传递函数的根轨迹分析:

一二阶可直接根据方程解的一般形式得到

三阶可根据渐近中心和渐近线得到.

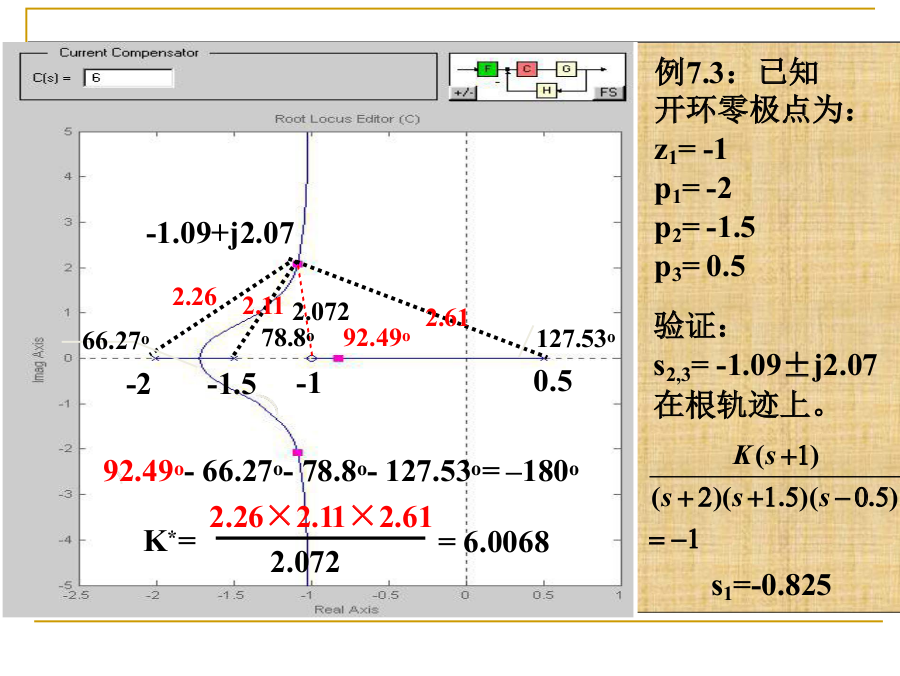
例子: 参数设计与分析

  1. 闭环系统稳定: 要求极点位于左半平面
  2. 稳定的欠阻尼系统: 包含复极点
  3. 主导为二阶系统的参数取值范围 (10倍): 满足极点距离的十倍关系

广义根轨迹

根据等效开环函数, 将想要调节的参数放到开环传递函数上方, 且位于系数位置, 之后正常进行考察.

控制器对根轨迹的影响

在前端添加控制器:

大致分为三类

  • 比例控制 KK
  • 微分控制 ss
  • 积分控制 1s\frac{1}{s}

三类控制器对二阶系统根轨迹的影响:

微分型控制器 K(s+z)K (s + z), 系统变为

K(s+z)(s+z1)(s+z2)\frac{K(s+z)}{(s + z_1)(s + z_2)}

结论: 增加合适的开环零点(足够右侧), 可以使根轨迹产生向左弯曲的倾向(弯曲靠近新添加的零点, 产生复根), 有利于提高系统稳定性和阻尼系数

积分型控制器 KKs+dK \frac{K}{s + d}, 系统变为

K(s+d)(s+z1)(s+z2)\frac{K}{(s + d)(s + z_1)(s + z_2)}

结论: 增加开环极点, 可以使根轨迹产生向右弯曲的倾向(渐近线从两条变成三条, 新极点的值影响渐近中心的值), 不利于系统稳定性, 但有利于稳态精度(型次变大)

综合型控制器 KK(s+z)s+dK \frac{K(s+z)}{s + d}, 系统变为

K(s+z)(s+d)(s+z1)(s+z2)\frac{K(s+z)}{(s + d)(s + z_1)(s + z_2)}

结论: 左侧的零 / 极点 占上风. 当零点占上风时, 轨迹向左弯曲; 极点占上风时, 轨迹向右弯曲.

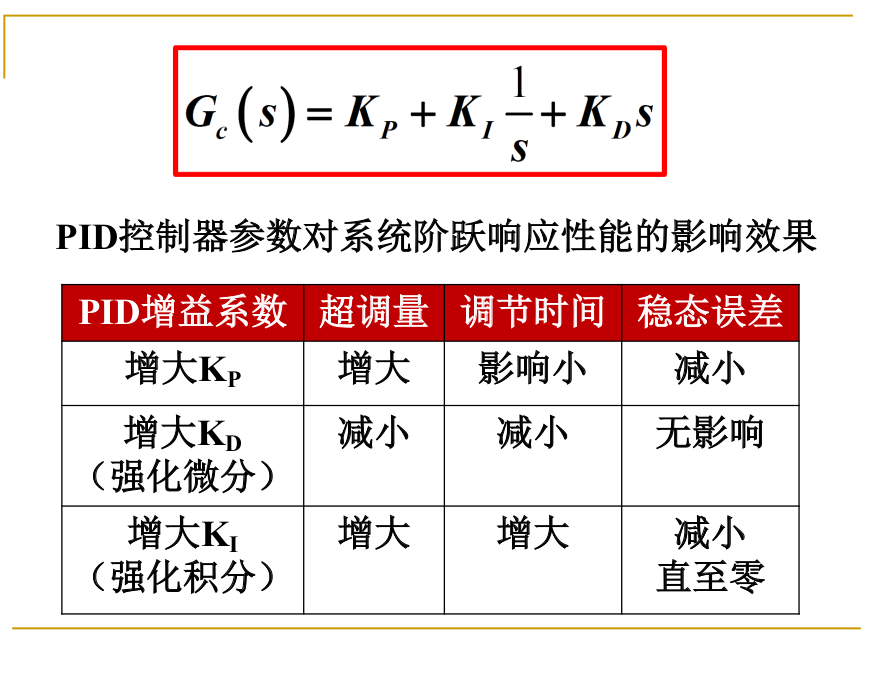
各种参数改变和系统性能的关系 (根据指标的等价线来记忆)
增大比例系数：

  • 超调量增大，
  • 调节时间不变，
  • 稳态误差减小，
  • 稳定性不变。

增大纯微分系数：

  • 出现过阻尼，
  • 调节时间变大，
  • 稳态误差不变，
  • 稳定性变差。

增大纯积分系数：

  • 超调量增大，
  • 调节时间变大，
  • 型次变大，改善稳态误差，
  • 稳定性变差，直至失稳。

PID控制器

基于根轨迹的控制系统设计

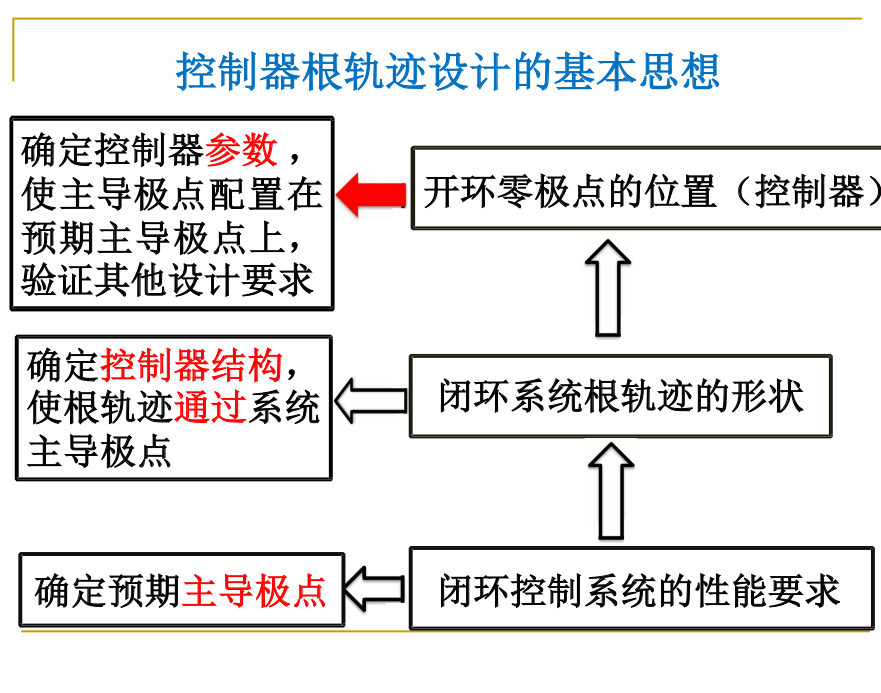
  1. 先分析性能要求, 得到零极点的可行域, 导出预期零极点
  2. 得到未矫正系统根轨迹图, 分析是否能配置到预期零极点上
  3. 确定控制器参数, 使主导极点配置在预期主导极点上, 同时考察此时各种指标是否符合
  4. 施加前置滤波器

课件中的三个实例.

MATLAB在根轨迹中的应用

绘制根轨迹

[r,K]=rlocus(sys)[r, K] = rlocus(sys)

分析根轨迹

rlocfind(sys)rlocfind(sys)

控制器设计

sisotool(G)sisotool(G)

backtop