[ControlSystem] Ch11 状态变量反馈控制系统设计

学习控制理论课程PPT的记录. 相关笔记会另开博客记录. 也可能不会开.

引言

能控性:
若存在无约束的控制信号 $u(t)$ , 能使系统从任意一个初始状态 $x(t_0)$ 转变到另一个预期状态 $x(t), t_0 \geq t \geq T$ , 这称该系统是完全能控的. (能控制系统转移到指定状态)

判别方法:

能控性秩判据: 对于n维连续时间线性时不变系统, 系统完全能控的充要条件为能控性判别矩阵 $P_c$ 满秩, 即

rank(P_c) = n, P_c = [B, AB, A^2B, ..., A^{n-1}B]

能观性:
当且仅当存在有限时间 $T$ , 给定控制变量 $u(t), 0\leq t \leq T$ 之后, 可以由 $y(t)$ 在 $[0, T]$ 上的观测值确定系统的初始状态 $x(0)$ , 则称系统是完全能观的. (能从输出的外在观测反推出内部状态)

能观性秩判据: 对于n维连续时间线性时不变系统, 系统完全能控的充要条件为能观性判别矩阵 $P_o$ 满秩, 即

rank(P_o) = n, P_c = [C, CA, CA^2, ..., CA^{n-1}]^T

基于状态反馈的极点配置方法:
反馈量不再是 $Hy$ , 而是 $Kx$ .

此时假设反馈需要的所有状态变量都可以直接测量.

当输入量 $r = 0$ 时, 系统为全状态反馈控制器. 输入信号 $u = -Kx$ , 状态方程为 $\dot x = Ax + Bu$ .

闭环系统状态方程为 $\dot x = (A - BK)x$

极点配置设计的问题在于: 选择合适的矩阵 $K$ , 将闭环系统状态矩阵 $A - BK$ 的特征值(即闭环控制系统的极点)配置到预定的位置

阿克曼公式:

K = [0, 0, ..., 1]P_c^{-1} q(A)

其中
$P_c$ 为能控性矩阵
$q(A)$ 为关于 $A$ 的多项式. 系数与期望的闭环系统的特征方程的系数相同.

设计步骤:

在状态量无法直接观测的情况下, 使用观测器来估计状态变量.

\dot {\hat{x}} = A \hat{x} + Bu + L(y - C \hat{x})

其中 $L$ 为观测器增益矩阵, 是观测器设计的核心.

对于估计误差 $e = x - \hat{x}$ , 我们有

\hat {e} = (A - LC)e

状态观测器的特征方程

det[\lambda I - (A - LC)] = 0

阿克曼公式:

K = P(A)P_o^{-1}[0, 0, ..., 1]^T

其中
$P_o$ 为能观性矩阵
$P(A)$ 为关于 $A$ 的多项式. 系数与期望的闭环系统的特征方程的系数相同.

设计步骤:

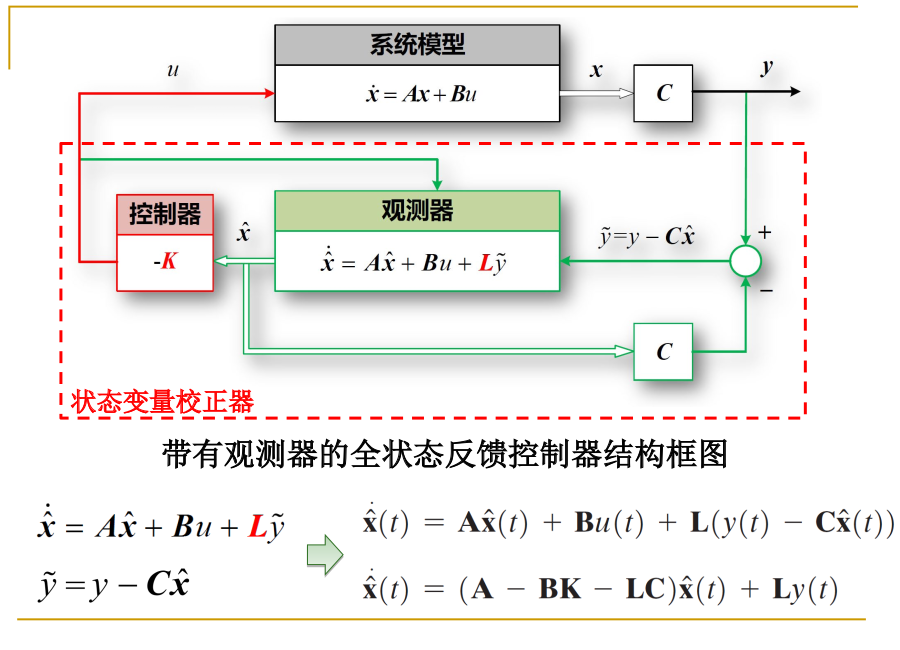
将观测器的结果作为全状态反馈.

方程为

\dot{\hat{x}} = A \hat{x} + Bu + L\hat{y}, \hat{y} = y - Cx

于是

\dot{\hat{x}} (t) = (A - BK - LC) \hat{x}(t) + L\hat{y} (t), u(t) = -K \hat{x}(t)

得到

\dot e = \dot x - \dot{\hat {x}} = (A - LC)e

\dot {x} = (A-BK)x + BKe

对应的特征多项式为

det(\lambda I - (A - BK)) det(\lambda I - (A - LC))

于是, 可以独立设置状态反馈控制器和状态观测器.

步骤:

U(s) = [-K(sI - (A - BK - LC))]^{-1}Y(s)

利用函数ctrb判断用状态空间模型描述的系统的能控性：
Pc = ctrb (A, B)
A是系统矩阵, B是输入矩阵, Pc 是能控性矩阵

利用函数obsv判断用状态空间模型描述的系统的能观性：
Po = obsv (A, C)
A是系统矩阵，C是输入矩阵，Po是能控性矩阵`

计算增益矩阵𝑲: 利用函数acker计算增益矩阵𝑲 K = acker(A, B, P)