[Automata] Ch9 Petri网络 PN

2024-12-17

LearnLog

学习Automata PPT的记录.

从哲学家吃面的情况引入: 随着哲学家数量的上涨, 使用迁移系统进行建模的难度呈指数级上升.

因此我们引入Petri 网, 用于描述这个并发调度问题.

Petri网

从自动机到Petri网

对于自动机, 它反应了一个牛顿式的世界观:

空间和时间作为绝对参考系；
过程视为该参考系下由时钟驱动。

在 Petri 网中

状态是分布式的，迁移是本地化的；
本地的因果关系取代了全局时间；
子系统之间通过显示的通信进行交互。

通过引入局部性的描述方法, 避免了全局建模时, 笛卡尔积导致的爆炸性增长问题.
利用了系统所具有的局部特性.

和状态机相比，Petri 网中的状态迁移是 不同步的(asynchronous) 。迁移的顺序是部分不协调的，由一个偏序关系规定。因此， Petri 网可以用来对并行的分布式系统进行建模。

各种类型的 Petri 网已经被广泛使用，比如说

活动图（Activity charts, UML）
数据流图（Data flow graphs）、标记图（marked graphs）

基本概念

二部图. 具有两种结点:

地点: 通常用来建模资源或者系统的部分状态
转移: 通常用来建模状态转换和同步.
图中的边是有向边, 且总是连接不同的结点 (好像红黑树? ). 在地点的资源被成为令牌.

形式化定义:
定义 Petri 网 是一个四元组 $C=(P,T,I,O)$ ，其中

$P$ 是地点的集合， $P={p1,p2, ...,pn}$ ；
$T$ 是转移的集合， $T={t1,t2, ... ,tm}$ ；
$I:T\rightarrow 2^P$ 是从迁移到输入地点的映射，一个迁移可以有不止一个输入地点；
$O:T\rightarrow 2^P$ 是从迁移到输出地点的映射，一个迁移可以有不止一个输出地点。

定义一张Petri网的标记 (marking) 为向量 $\mu = <\mu_1, \mu_2, ..., \mu_n>$
其中每个分量表示地点上的令牌 (token)数量.

点火 fire

我们称一个转移 $t$ 在特定的标记 $\mu$ 下是 被赋能的(enabled) ，如果对于从任意地点 $p$ 到 $t$ 的弧，在该标记 $\mu$ 下 $p$ 中都存在一个令牌。

即, 在这个标记下, 该转移所对应的 "源结点"都持有至少一个资源 / 令牌

一个在 $\mu$ 下被赋能的转移 $t$ 可以 点火(fire) ，导致一个新的标记 $\mu'$ 。

点火(fire) 一个被赋能的转移 $t$ 会导致两件事情发生：

对于每一个从地点 $p$ 到转移 $t$ 的弧，从地点 $p$ 中减去一个令牌；
对于每一个从转移 $t$ 到地点 $p$ 的弧，向地点 $p$ 中增加一个令牌。

记恰好赋能 $t$ 的标记为 $\cdot t$ ， $\cdot t$ 中有且仅有让 $t$ 点火一次所必要的令牌， $\cdot t$ 在 $t$ 点火一次后变成 $t \cdot$ 。于是在 $\mu$ 标记状态下点火 $t$ 变成 $\mu'$ 标记的过程可以形式化表述为：

\mu '=(\mu - \cdot t)+t\cdot

即, 点火一次相当于"进行了一次转移".
(这里的向量化表述挺有意思的)

Ex: 可以将化学反应的过程也视为点火的过程. (添加上一些带权边)

Petri 网的一次 运行(run) 是一个有穷的或者无穷的标记和转移的序列，形如

\mu_0 \rightarrow ^{t_0} \mu_1 \rightarrow ^{t_1} ... \rightarrow ^{t_n-1} \mu_n \rightarrow ^{t_n} ...

其中， $\mu 0$ 是 Petri 网的初始状态，对于任意 $i\geq 0$ ， $ti \in enabled(\mu i)$ ， $enabled(\mu i)$ 表示在 $\mu i$ 状态下被赋能的转移的集合，且

\mu i​=(\mu i -1​ -\cdot ti-1)+ti-1​

即每一次状态转换都是由于一个迁移的点火而产生的。

此处, Petri网的"状态"相当于令牌标记, 而转移相当于一个个转移的向量.
对于n个地点, 整个过程用n维向量建模

Petri网的性质

基本性质

某些结构所具有的有趣性质

顺序执行（Sequential Execution）转移 $t2$ 只会在转移 $t1$ 点火后点火。这形成了一个优先级限制： $t2$ 在 $t1$ 之后。
同步（Synchronization）: 转移 $t1$ 只有在它的每一个输入地点都至少有一个令牌的时候才会被激活。
汇合（Merging）:当来自多个地方的令牌通过同一个转移的点火到达一个地方的时候，汇合发生了。
分叉（Fork）:当来自一个个地方的令牌通过一个转移的点火到达多个地方的时候，分叉发生了。
并发（Concurrency）: $t1$ 和 $t2$ 是并发的，由于这个性质， Petri网可以建模分布式控制、多进程同时运行的系统。
非确定性发展（Non-deterministic Evolution）: Petri 网的发展是非确定性的，被赋能的任意一个转移都可能点火。(符合并发的性质)
冲突（conflict）: $t1$ 和 $t2$ 都被赋能了，但是任意一方点火都会导致另一方无法点火。

扩展和规约

一些定义:

源转移（source transition）：没有输入。
槽转移（sink transition）：没有输出。
自环（self-loop）：一个二元组 $(p,t)$ ，其中 $p$ 即是 $t$ 的一个输入，也是 $t$ 的一个输出。
纯 Petri 网（pure PN）：没有自环。
带权 Petri 网（weighted PN）：弧上有权重
普通 Petri 网（ordinary PN）：所有的弧的权重都是 1
无限容量网（infinite capacity net）：地点可以存放的令牌数没有限制
有限容量网（finite capacity net）：每个地点 $p$ 有一个最大容量 $K(p)$
严格转移规则（strict transition rule）：在点火后，每一个输出地点 $p$ 都不可以拥有多于 $K(p)$ 个令牌。

TH 每一个有限容量网都可以转换为一个等价的纯的无限容量网.

换言之, 赋予网络自环和容量限制, 并没有扩展网络的表达能力.

证明:
等价性: 所有可能的点火序列的集合是同一个集合. (类似状态机的定义, 只不过此时着重考虑转移, 而不强调节点)

解自环: 对于自环(同时作为某个转移源节点和目标节点的情况. ), 添加一个 dummy place和 dummy transition. 于是在去除自环的同时, 网络与原来的网络是等价的

去除容量限制: 对每一个具有容量限制的地点, 添加一个补地点 complementary place. 该地点的初始令牌量为原地点的补, 同时转移与原地点的转移构成环. (对于每一个出边和入边, 都构造相应的"补边"). 此时, 去除原始节点的容量限制, 行为上的容量限制由补节点来完成

Petri 网的应用实例

可以用来建模一些并发场景下, 各进程之间的限制和制约关系.

例如, 单轨铁路下, 两辆火车的运行限制; 通信协议的发送和接收过程; 餐厅服务员接收顾客点单和上菜过程; 自动售货机; 生产流水线; 哲学家吃面问题等.

此时, 建模哲学家吃面问题的节点数量就从原来的指数级别缩减到了线性级别. (因为此时的节点数量用于表示"局部状态", 全局状态被隐含在 marking中)

Petri 网进阶

行为性质

可达性 Reachability:

若存在一个点火序列将一个Marking A转换为另一个B, 则称 B从A可达.
可达性可判定, 但是需要指数时间.

有界性 Boundedness:

一个Petri 网是k有界的, 如果 $M_0$ 可达的所有标记中, 每个地点的令牌数量都不超过一个有限数字k (即, marking的无穷范数不超过k)
若一个Petri网1 有界, 则称其是安全的.

活跃性 Liveness:

一个 Petri 网是活跃的，如果无论它现在到达了怎样的标记，总是有可能通过一个合适的点火序列点火任何转移。
等价于不存在死锁
看得有些迷惑. 事实上这里的定义省略了很多内容.

以下概念摘自wiki百科:
Liveness

Petri nets can be described as having different degrees of liveness L1−L4 ${isplaystyle L_{1}-L_{4}}$ . A Petri net (N,M0) ${isplaystyle (N,M_{0})}$ is called Lk ${isplaystyle L_{k}}$ -live if and only if all of its transitions are Lk ${isplaystyle L_{k}}$ -live, where a transition is

dead, if it can never fire, i.e. it is not in any firing sequence in L(N,M0) ${isplaystyle L(N,M_{0})}$
L1 ${isplaystyle L_{1}}$ -live (potentially fireable), if and only if it may fire, i.e. it is in some firing sequence in L(N,M0) ${isplaystyle L(N,M_{0})}$
L2 ${isplaystyle L_{2}}$ -live if it can fire arbitrarily often, i.e. if for every positive integer k, it occurs at least k times in some firing sequence in L(N,M0) ${isplaystyle L(N,M_{0})}$
L3 ${isplaystyle L_{3}}$ -live if it can fire infinitely often, i.e. if there is some fixed (necessarily infinite) firing sequence in which for every positive integer k, the transition L3 ${isplaystyle L_{3}}$ occurs at least k times,
L4 ${isplaystyle L_{4}}$ -live (live) if it may always fire, i.e. it is L1 ${isplaystyle L_{1}}$ -live in every reachable marking in R(N,M0) ${isplaystyle R(N,M_{0})}$

Note that these are increasingly stringent requirements: Lj+1 ${isplaystyle L_{j+1}}$ -liveness implies Lj ${isplaystyle L_{j}}$ -liveness, for j∈1,2,3 ${extstyle extstyle {jn {1,2,3}}}$ .

These definitions are in accordance with Murata’s overview, which additionally uses L0 ${isplaystyle L_{0}}$ -live as a term for dead.

可逆性 Reversibility:

一个Petri 网是可逆的, 如果对于每一个从 $M_0$ 可达的标记, 它也能返回 $M_0$
更宽松的条件: 对于每一个从 $M_0$ 可达的标记, 它能够返回一个被标记的home state $M '$

持续性（Persistence）

一个 Petri 网是持续的，如果任意两个被赋能的转移，其中一个的点火都不会让另一个失能（disable）；
如此，一旦一个转移被赋能，直到被点火之前它会一直被赋能。

公平性（fairness）

有界公平性（bounded-fairness）：一个转移可以点火但另一个转移不能点火的数量是有界的，即冲突的数量是有界的。
无条件公平性（unconditional-fairness）：每一个转移在一个点火序列中都可以无穷经常（infinitely often）出现。

分析方法

导入覆盖树和覆盖图. 相当于将原本隐式的marking状态和对应的转移做显示地展开.

覆盖树（coverability tree）是所有可能的标记的树形表示：

根结点为 $M_0$ ；
树上的结点是从 $M_0$ 可达的标记；
树的边是转移的点火。

若一张Petri网是无界的, 可以引入 $\omega$ 来判断覆盖树是否有界. $\omega$ 代表那些拥有无限令牌的地点.

通过覆盖树来判断 Petri 网的各种性质. 推导是通过定义自然得到的.

一个 Petri 网是有界的，当且仅当 $w$ 不出现在覆盖树的任何的结点中；
一个 Petri 网是安全的，当且仅当只有 0 和 1 出现在覆盖树的结点中；
一个转移是死的，当且仅当它不出现在覆盖树的任何的边中；
如果 $M$ 从 $M_0$ 可达，那么存在一个结点 $M′$ 可以覆盖 $M$ 。 (此处的覆盖代表什么意思? 也许树中的节点实际表达的是marking的集合? 一族marking?)

规约规则

由于分析的复杂度会随着Petri 网的大小而指数级增长. 因此, 我们可以在保证要分析的性质不变的情况下, 化简 Petri网. 主要是以下性质:

活跃性（liveness）
安全性（safeness）
有界性（boundedness）

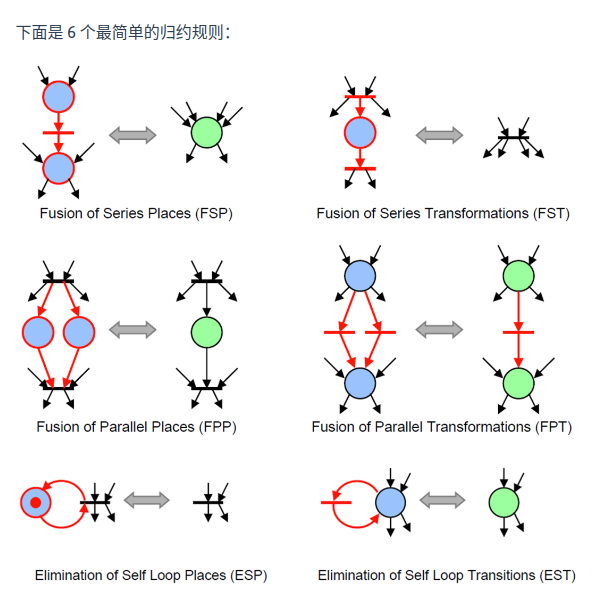
广义扩展

染色 Petri 网（colored petri nets）：令牌可以带有值（颜色），任何具有有限种颜色的 Petri 网都可以转化成一个普通的 Petri 网。
连续 Petri 网（continuous petri nets）：令牌的数量可以是实数，不可以被转化成一个普通的 Petri 网。
抑制弧（inhibitor arcs）：在一个地点没有令牌的时候为转移赋能，不可以被转化成一个普通的 petri 网。
时间扩展: 为了能够对这些和时间相关的性质建模，我们需要向已有的形式化系统中引入一个时间的量化记号。

时间 Petri 网

时间 Petri 网（time petri nets）在经典的 Petri 网的每一个转移中关联了一个时间区间 $[a,b]$ 。

假设 $t$ 在时间 $c$ 被赋能，那么 $t$ 只能在时间区间 $[c+a,c+b]$ 内点火，且最迟必须在时间 $c+b$ 点火，除非它因为其他转移的点火而失能了。

即, 赋能一段时间后必须强制点火, 除非在此之前失能.

一个转移的点火本身不消耗时间。

一个时间 Petri 网是一个 6 元祖， $N=(P,T,F,Eft,Lft,\mu 0)$ ，其中

$P={p1,p2,...,pn}$ 是一个地点的有限集；
$T={t1,t2,...,tn}$ 是一个转移的有限集（ $P\cap T=\emptyset P \cap T=\emptyset$ ）
$F \subseteq (P\times T)\cap(T\times P)$ 是流关系（flow relation）；
$Eft,Lft:T\rightarrow N$ 是求转移的最早点火时间和最迟点火时间的函数，满足 $\forall t\in T,Eft(t)\leq Lft(t)\leq \infty \forall t \in T,Eft(t)\leq Lft(t)\leq \infty$ ；
$\mu 0$ 是这张网的初始标记。

此处对应转移的描述是通过flow relation (边)来完成的, 而非之前的函数形式. 更加符合对于图的描述方法 (先描述节点, 再描述边, 然后描述时间函数和起始标记)

此时, 网络的状态由一个二元组描述 $s = (\mu, c)$ . 其中 $c: enabled(\mu) \rightarrow T$ 称为时钟函数 (定义域为被赋能的转移的集合, 值域为时间域, 一般令为非负实数集)

一个转移 $t$ 可以从状态 $s=(\mu,c)$ 在延时 $\delta \in T$ 后点火当且仅当下列条件满足：

$t\in enabled(\mu)$ ，即 $t$ 应当处于激活状态
$(\mu - \cdot t)\cap t \cdot =\emptyset$ ，即 $t$ 点火后, 将前往的地点不应该已有令牌 (网络始终处于安全状态)
$Eft(t)\leq c(t)+\delta$ ，即 $t$ 点火时间应当满足最早要求
$\forall t' \in enabled(\mu):c(t')+\delta \leq Lft(t')$ 。即当前marking的所有转移都不应当违背点火时间俺的最迟要求. (满足最早要求的前提下, 越早越好)

当转移 $t$ 在 $\delta$ 延迟后从状态 $s=(\mu,c)$ 点火，新状态 $s'=(\mu',c')$ 为：

$\mu'=(\mu−\cdot t)∪t\cdot$
$\forall t'\in enabled(\mu')$ ，如果 $t' \neq t$ 且 $t' \in enabled(\mu)$ ，则 $c'(t')=c(t')+\delta$ ，否则 $c'(t')=0$ 。对于新marking的已经激活的转移, 如果它属于"前朝遗老", 则时间继承不变; 否则时间清零. (记录每个转移被激活的时间点, 即是"早就被激活"还是"刚刚被激活")

关于同时点火

在不带时间的 Petri 网中，同时点火（不冲突的转移之间）的表示是不相关的。序列上虽然有先后的顺序, 但是只是逻辑上的而不是时间上的, 因为没有时间的定义.

而在带时间的模型中, “同时点火"可以确实是"同时的”. 此处的同时不是逻辑上的而确实是时间上的, 没有逻辑上的先后关系. 当然, 在某些情况下, "时间上同时"而"逻辑上不同时"的情况是可能发生的. 此时虽然点火的时刻是相同的, 但是点火的序列上需要符合先后关系.

延时下界为 $0$ 的转移也称为之零时转移（zero-time transitions），因为他们可以在被赋能的同时点火，没有延迟。零时转移如果不小心处理，可能会导致 Zeno 行为 —— 时间停滞。即, 虽然在模型中转移不断地接连发生, 但是时间却一直停滞没有增长. 这在物理上是不可能的.

例子: 简化的火车道口

在给定火车前进时间以及门的开启 / 关闭时间的前提下, 保证火车通过相应路段的时候道口门总是关闭的 (防止行人和车辆进入 . )